
【題目】2020年春季,某出租汽車公司決定更換一批新的小汽車以代替原來報廢的出租車,現有![]() 兩款車型,根據以往這兩種出租車車型的數據,得到兩款出租車車型使用壽命頻數表如下:
兩款車型,根據以往這兩種出租車車型的數據,得到兩款出租車車型使用壽命頻數表如下:
使用壽命年數 | 5年 | 6年 | 7年 | 8年 | 總計 |
| 10 | 20 | 45 | 25 | 100 |
| 15 | 35 | 40 | 10 | 100 |
(1)填寫下表,并判斷是否有![]() 的把握認為出租車的使用壽命年數與汽車車型有關?
的把握認為出租車的使用壽命年數與汽車車型有關?
使用壽命不高于 | 使用壽命不低于 | 總計 | |
| |||
| |||
總計 |
(2)司機師傅小李準備在一輛開了![]() 年的
年的![]() 型車和一輛開了
型車和一輛開了![]() 年的
年的![]() 型車中選擇,為了盡最大可能實現
型車中選擇,為了盡最大可能實現![]() 年內(含
年內(含![]() 年)不換車,試通過計算說明,他應如何選擇.
年)不換車,試通過計算說明,他應如何選擇.
附: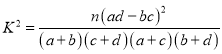 ,
,![]() .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
【答案】(1)填表見解析;有![]() 的把握認為出租車的使用壽命年數與汽車車型有關;
的把握認為出租車的使用壽命年數與汽車車型有關;
(2)小李應選擇![]() 型出租車
型出租車
【解析】
(1)根據表格,把使用壽命不高于![]() 年和使用壽命不低于
年和使用壽命不低于![]() 年的
年的![]() 型、
型、![]() 型車分別求和,填表即可,把數據代入公式計算出卡方,然后同臨界值比較作出結論即可. (2)分別計算出
型車分別求和,填表即可,把數據代入公式計算出卡方,然后同臨界值比較作出結論即可. (2)分別計算出![]() 型、
型、![]() 型車
型車![]() 年內(含
年內(含![]() 年)使用壽命的概率,取概率小的即可.
年)使用壽命的概率,取概率小的即可.
解:(1)填表如下:
使用壽命不高于 | 使用壽命不低于 | 總計 | |
| 30 | 70 | 100 |
| 50 | 50 | 100 |
總計 | 80 | 120 | 20 |
由列聯表可知![]() ,
,
故有![]() 的把握認為出租車的使用壽命年數與汽車車型有關.
的把握認為出租車的使用壽命年數與汽車車型有關.
(2)記事件![]() 分別表示小李選擇
分別表示小李選擇![]() 型出租車和
型出租車和![]() 型出租車時,
型出租車時,![]() 年內(含
年內(含![]() 年)換車.
年)換車.
由表知![]() ,
,
![]() ,
,
![]() ,故小李應選擇
,故小李應選擇![]() 型出租車.
型出租車.


 全優考典單元檢測卷及歸類總復習系列答案
全優考典單元檢測卷及歸類總復習系列答案科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,側棱
中,側棱![]() 底面
底面![]() ,
,![]()
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 是棱
是棱![]() 中點.
中點.
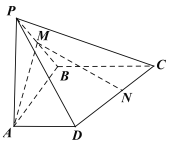
(1)已知點![]() 在棱
在棱![]() 上,且平面
上,且平面![]() 平面
平面![]() ,試確定點
,試確定點![]() 的位置并說明理由;
的位置并說明理由;
(2)設點![]() 是線段
是線段![]() 上的動點,當點
上的動點,當點![]() 在何處時,直線
在何處時,直線![]() 與平面
與平面![]() 所成角最大?并求最大角的正弦值.
所成角最大?并求最大角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 是直角梯形且
是直角梯形且![]() ∥
∥![]() ,側面
,側面![]() 為等邊三角形,且平面
為等邊三角形,且平面![]() 平面
平面![]() .
.
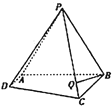
(1)求平面![]() 與平面
與平面![]() 所成的銳二面角的大小;
所成的銳二面角的大小;
(2)若![]() ,且直線
,且直線![]() 與平面
與平面![]() 所成角為
所成角為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某射擊運動員在比賽前進行三周的封閉訓練,教練員將其每天成績的均值數據整理,并繪成條形圖如下,
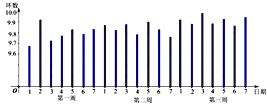
根據該圖,下列說法錯誤的是:( )
A.第三周平均成績最好B.第一周平均成績比第二平均成績好
C.第一周成績波動較大D.第三周成績比較穩定
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在①![]() ,②
,②![]() ,③
,③![]() 這三個條件中任選一個,補充在下面問題中,并解答.
這三個條件中任選一個,補充在下面問題中,并解答.
已知等差數列![]() 的公差為
的公差為![]() ,等差數列
,等差數列![]() 的公差為
的公差為![]() .設
.設![]() 分別是數列
分別是數列![]() 的前
的前![]() 項和,且
項和,且![]() , ,
, ,
(1)求數列![]() 的通項公式;
的通項公式;
(2)設![]() ,求數列
,求數列![]() 的前
的前![]() 項和
項和![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】記無窮數列![]() 的前n項
的前n項![]() ,
,![]() ,…,
,…,![]() 的最大項為
的最大項為![]() ,第n項之后的各項
,第n項之后的各項![]() ,
,![]() ,…的最小項為
,…的最小項為![]() ,
,![]() .
.
(1)若數列![]() 的通項公式為
的通項公式為![]() ,寫出
,寫出![]() ,
,![]() ,
,![]() ;
;
(2)若數列![]() 的通項公式為
的通項公式為![]() ,判斷
,判斷![]() 是否為等差數列,若是,求出公差;若不是,請說明理由;
是否為等差數列,若是,求出公差;若不是,請說明理由;
(3)若數列![]() 為公差大于零的等差數列,求證:
為公差大于零的等差數列,求證:![]() 是等差數列.
是等差數列.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知平面直角坐標系![]() 中,過點
中,過點![]() 的直線
的直線![]() 的參數方程為
的參數方程為![]() (t為參數),
(t為參數),![]() 與y軸交于A,以該直角坐標系的原點O為極點,
與y軸交于A,以該直角坐標系的原點O為極點,![]() 軸的非負半軸為極軸建立極坐標系.曲線C的極坐標方程
軸的非負半軸為極軸建立極坐標系.曲線C的極坐標方程![]() ,直線
,直線![]() 與曲線C交于M、N兩點.
與曲線C交于M、N兩點.
(1)求曲線C的直角坐標方程和點A的一個極坐標;
(2)若![]() ,求實數m的值.
,求實數m的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com