分析:(1)先利用點A在圓上求出m,再利用直線PF
1與圓C相切求出直線PF
1與的方程以及c,再利用點A在橢圓上求出2a,即可求出橢圓E的方程;
(2)先把
•用點Q的坐標表示出來,再利用Q為橢圓E上的一個動點以及基本不等式即可求出
•的取值范圍.
解答:解:(1)點A代入圓C方程,得(3-m)
2+1=5.
∵m<3,
∴m=1.
設直線PF
1的斜率為k,
則PF
1:y=k(x-4)+4,即kx-y-4k+4=0.
∵直線PF
1與圓C相切,圓C:(x-1)
2+y
2=5,
∴
=,
解得
k=,或k=.
當k=
時,直線PF
1與x軸的交點橫坐標為
,不合題意,舍去.
當k=
時,直線PF
1與x軸的交點橫坐標為-4,
∴c=4.
∴F
1(-4,0),F
2(4,0).
故2a=AF
1+AF
2=
5+=6,
a=3,a
2=18,b
2=2.
橢圓E的方程為:
+=1.
(2)
=(1, 3),設Q(x,y),
=(x-3, y-1),
•=(x-3)+3(y-1)=x+3y-6.
∵
+=1,即x
2+(3y)
2=18,而x
2+(3y)
2≥2|x|•|3y|,
∴-18≤6xy≤18.
則(x+3y)
2=x
2+(3y)
2+6xy=18+6xy的取值范圍是[0,36].
∴x+3y的取值范圍是[-6,6]
∴x+3y-6的范圍只:[-12,0].
即
•的取值范圍是[-12,0].
點評:本題是對圓與橢圓知識的綜合考查.當直線與圓相切時,可以利用圓心到直線的距離等于半徑求解.,也可以把直線與圓的方程聯立讓對應方程的判別式為0求解.

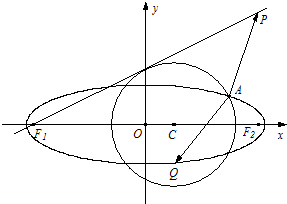 已知點P(4,4),圓C:(x-m)2+y2=5(m<3)與橢圓E:
已知點P(4,4),圓C:(x-m)2+y2=5(m<3)與橢圓E:

 已知點P(4,4),圓C:(x-m)2+y2=5(m<3)與橢圓E:
已知點P(4,4),圓C:(x-m)2+y2=5(m<3)與橢圓E: 已知點P (4,4),圓C:(x-m)2+y2=5(m<3)與橢圓E:
已知點P (4,4),圓C:(x-m)2+y2=5(m<3)與橢圓E: 已知點P(4,4),圓C:(x-m)2+y2=5(m<3)與橢圓E:
已知點P(4,4),圓C:(x-m)2+y2=5(m<3)與橢圓E: 與橢圓E:
與橢圓E: 有一個公共點A(3,1),F1.F2分別是橢圓的左.右焦點,直線PF1與圓C相切.
有一個公共點A(3,1),F1.F2分別是橢圓的左.右焦點,直線PF1與圓C相切.
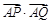 的范圍.
的范圍.