
已知函數f (x)=x3+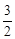 (1-a)x2-3ax+1,a>0.
(1-a)x2-3ax+1,a>0.
(Ⅰ) 證明:對于正數a,存在正數p,使得當x∈[0,p]時,有-1≤f (x)≤1;
(Ⅱ) 設(Ⅰ)中的p的最大值為g(a),求g(a)的最大值.
(Ⅰ)先利用導數求出單調區間,再分情況證明;
(Ⅱ) 
【解析】
試題分析:
(Ⅰ) 由于f ′(x)=3x2+3(1-a)x-3a=3(x+1)(x-a),且a>0,
故f (x)在[0,a]上單調遞減,在[a,+∞)上單調遞增.
又f (0)=1,f (a)=-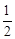 a3-
a3-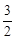 a2+1=
a2+1=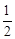 (1-a)(a+2) 2-1.
(1-a)(a+2) 2-1.
當f (a)≥-1時,取p=a.
此時,當x∈[0,p]時有-1≤f (x)≤1成立.
當f (a)<-1時,由于f (0)+1=2>0,f (a)+1<0,
故存在p∈(0,a)使得f (p)+1=0.
此時,當x∈[0,p]時有-1≤f (x)≤1成立.
綜上,對于正數a,存在正數p,使得當x∈[0,p]時,有-1≤f (x)≤1. 7分
(Ⅱ) 由(Ⅰ)知f (x)在[0,+∞)上的最小值為f (a).
當0<a≤1時,f (a)≥-1,則g(a)是方程f (p)=1滿足p>a的實根,
即2p2+3(1-a)p-6a=0滿足p>a的實根,所以
g(a)=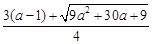 .
.
又g(a)在(0,1]上單調遞增,故g(a)max=g(1)= .
.
當a>1時,f (a)<-1.
由于f (0)=1,f (1)=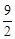 (1-a)-1<-1,故[0,p]Ì [0,1].
(1-a)-1<-1,故[0,p]Ì [0,1].
此時,g(a)≤1.
綜上所述,g(a)的最大值為 . 15分
. 15分
考點:本題主要考查利用導數研究函數的性質等基礎知識,同時考查推理論證能力,分類討論等綜合解題能力和創新意識。
點評:研究函數的性質往往離不開導數,導數是研究函數性質的有力工具,要靈活運用;另外,函數如果含參數,一般離不開分類討論,分類討論時要做到不重不漏.


科目:高中數學 來源:2011屆南京市金陵中學高三第四次模擬考試數學試題 題型:解答題
(本小題滿分16分)已知函數f(x)=ax2-(2a+1)x+2lnx(a為正數).
(1) 若曲線y=f(x)在x=1和x=3處的切線互相平行,求a的值;
(2) 求f(x)的單調區間;
(3) 設g(x)=x2-2x,若對任意的x1∈(0,2],均存在x2∈(0,2],使得f(x1)<g(x2),求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源:2010-2011學年浙江省杭州市高三上學期開學考試數學卷 題型:選擇題
已知函數f(x)=4x2-mx+5在區間[-2,+∞)上是增函數,則f(1)的范圍是( )
A.f(1)≥25 B.f(1)=25 C.f(1)≤25 D.f(1)>25
查看答案和解析>>
科目:高中數學 來源:2010-2011學年湖北省天門市高三天5月模擬文科數學試題 題型:填空題
已知函數f(x)=ax2+bx+c(a≠0),且f(x)=x無實根,下列命題中:
(1)方程f [f (x)]=x一定無實根;
(2)若a>0,則不等式f [f (x)]>x對一切實數x都成立;
(3)若a<0,則必存在實數x0,使f [f (x0)]>x0;
(4)若a+b+c=0,則不等式f [f (x)]<x對一切x都成立;
正確的序號有 .
查看答案和解析>>
科目:高中數學 來源:2012屆江西省南昌市高三第一次模擬測試卷理科數學試卷 題型:選擇題
已知函數f(x)=|lg(x-1)|-( )x有兩個零點x1,x2,則有
)x有兩個零點x1,x2,則有
A.x1x2<1 B.x1x2<x1+x2
C.x1x2=x1+x2 D.x1x2>x1+x2
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com