已知圓E經過點A(2,-3)、B(-2,-5),且圓心在直線x-2y-3=0上.
(1)求圓E的方程;
(2)若直線x+y+m=0與圓E交于P、Q兩點,且 EP⊥EQ,求m的值.
【答案】
分析:(1)根據圓心E在直線x-2y-3=0,可設圓心E( 2b+3,b ),由|EA|=|EB|列出方程解出 b=-2,求得圓心E的坐標即半徑,從而得到圓的標準方程.
(2)設圓心到直線的距離為d,由題意可得
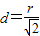
,即
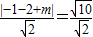
,解此方程求出m的值.
解答:解:(1)∵圓心E在直線x-2y-3=0,可設圓心E(2b+3,b ).
由|EA|=|EB|可得
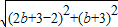
=
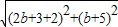
,
平方化簡可得 5b
2+10b+10=5b
2+30b+30,
解得 b=-2,故點E(-1,-2).
由兩點間距離公式得r
2 =|EA|
2=10,
所以,圓的方程為(x+1)
2+(y+2)
2=10.
(2)由題意可得△EPQ為等腰直角三角形,EP=EQ=r=
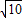
,
設圓心到直線PQ的距離為d,可得
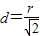
,
再由點E(-1,-2),PQ的方程為x+y+m=0,故有
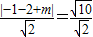
,
解得
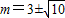
.
點評:本題主要考查求圓的標準方程的方法,求出圓心坐標和半徑的值,是解題的關鍵.直線和圓的位置關系,點到直線的距離公式的應用,屬于中檔題.

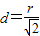 ,即
,即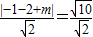 ,解此方程求出m的值.
,解此方程求出m的值.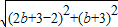 =
=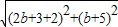 ,
,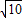 ,
,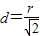 ,
,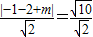 ,
,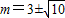 .
.

 英才點津系列答案
英才點津系列答案 紅果子三級測試卷系列答案
紅果子三級測試卷系列答案 課堂練加測系列答案
課堂練加測系列答案 (2012•江蘇)A.[選修4-1:幾何證明選講]
(2012•江蘇)A.[選修4-1:幾何證明選講]