
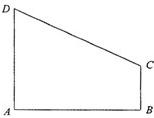
 如圖,直角梯形ABCD中∠DAB=90°,AD∥BC,AB=2,AD=
如圖,直角梯形ABCD中∠DAB=90°,AD∥BC,AB=2,AD=| 3 |
| 2 |
| 1 |
| 2 |
| EC |
| 1 |
| 2 |
| AB |
| b2 |
| a |
| 3 |
| 2 |
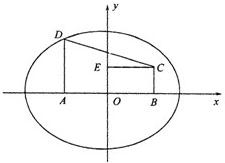 解:(Ⅰ)如圖,以AB所在直線為x軸,
解:(Ⅰ)如圖,以AB所在直線為x軸,| x2 |
| a2 |
| y2 |
| b2 |
| b2 |
| a |
|
|
| x2 |
| 4 |
| y2 |
| 3 |
| EC |
| 1 |
| 2 |
| AB |
| 1 |
| 2 |
|
| x1+x2 |
| 2 |
| 4km |
| 3+4k2 |
| 3m |
| 3+4k2 |
y0-
| ||
| x0 |
| 1 |
| k |
| ||||
-
|
| 1 |
| k |
| 3+4k2 |
| 2 |
| 3+4k2 |
| 2 |
| π |
| 4 |


科目:高中數(shù)學 來源: 題型:
 (2014•宜賓一模)如圖,直角梯形ABCD中,∠ABC=∠BAD=90°,AB=BC且△ABC的面積等于△ADC面積的
(2014•宜賓一模)如圖,直角梯形ABCD中,∠ABC=∠BAD=90°,AB=BC且△ABC的面積等于△ADC面積的| 1 | 2 |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
 (2013•惠州一模)如圖,直角梯形ACDE與等腰直角△ABC所在平面互相垂直,F(xiàn)為BC的中點,∠BAC=∠ACD=90°,AE∥CD,DC=AC=2AE=2
(2013•惠州一模)如圖,直角梯形ACDE與等腰直角△ABC所在平面互相垂直,F(xiàn)為BC的中點,∠BAC=∠ACD=90°,AE∥CD,DC=AC=2AE=2查看答案和解析>>
科目:高中數(shù)學 來源:2011-2012學年江西省南昌市高三第二次模擬測試理科數(shù)學試卷(解析版) 題型:解答題
(本小題滿分12分)如圖:直角梯形ABCD中,AD∥BC,∠ABC=90°,E、F分別是邊AD和BC上的點,且EF∥AB,AD =2AE =2AB = 4AF= 4,將四邊形EFCD沿EF折起使AE=AD.
(1)求證:AF∥平面CBD;
(2)求平面CBD與平面ABFE夾角的余弦值.

查看答案和解析>>
科目:高中數(shù)學 來源:2013年廣東省惠州市高考數(shù)學一模試卷(文科)(解析版) 題型:解答題

查看答案和解析>>
科目:高中數(shù)學 來源:2012年寧夏銀川市賀蘭一中高考數(shù)學一模試卷(理科)(解析版) 題型:解答題
 .梯形ABCD所在平面外有一點P,滿足PA⊥平面ABCD,PA=PB.
.梯形ABCD所在平面外有一點P,滿足PA⊥平面ABCD,PA=PB.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com