為響應政府“還家鄉青山綠水,走生態發展之路”的號召,某縣兩村F1、F2準備種植圍繞村莊的防護林,如圖,在與兩個村同一條直線上有兩個機井A1,A2,兩村在兩個機井之間,每個村到兩機井的距離都分別為3千米與1千米,根據現有地理特點,兩村擬定每個種植點距兩村距離和等于兩機井間距離.
(Ⅰ)請你利用所學知識,建立適當的平面直角坐標系,求出種植點所在的曲線方程;
(Ⅱ)已知過F2村有一條小路l,且斜率為1,試求在小路l上的兩個種植點間距離.
【答案】
分析:(Ⅰ)以A
1A
2所在直線為x軸,線段A
1A
2的垂直平分線為y軸,建立平面直角坐標系,根據兩村擬定每個種植點距兩村距離和等于兩機井間距離,兩機井間距離為10千米,由橢圓的定義可知,種植點所在的曲線為以A
1A
2為長軸,F
1、F
2為焦點的橢圓,從而可得種植點所在的曲線方程;
(Ⅱ)小路l所在直線方程為:y=x-1,代入橢圓方程,求出交點坐標,利用兩點間的距離公式,即可得到結論.
解答:解:(Ⅰ)以A
1A
2所在直線為x軸,線段A
1A
2的垂直平分線為y軸,建立平面直角坐標系.
∵兩村擬定每個種植點距兩村距離和等于兩機井間距離,兩機井間距離為10千米
∴由橢圓的定義可知,種植點所在的曲線為以A
1A
2為長軸,F
1、F
2為焦點的橢圓
設橢圓方程為:
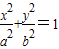
(a>b>0),則a+c=3,a-c=1,所以a=2,c=1,b=

=
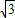
.
∴種植點所在的曲線方程為
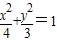
;
(Ⅱ)由題意,小路l所在直線方程為:y=x-1,代入橢圓方程,消去y可得7x
2-8x-8=0
∴x=
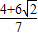
或x=

∴y=
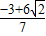
或y=
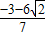
∴兩點之間距離為
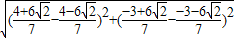
=
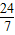
即在小路l上的兩個種植點間距離為
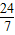
千米.
點評:本題考查利用數學知識解決實際問題,考查直線與橢圓的位置關系,考查學生的計算能力,屬于中檔題.

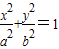 (a>b>0),則a+c=3,a-c=1,所以a=2,c=1,b=
(a>b>0),則a+c=3,a-c=1,所以a=2,c=1,b= =
=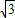 .
.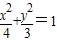 ;
;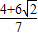 或x=
或x=
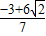 或y=
或y=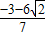
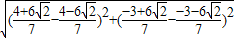 =
=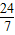
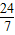 千米.
千米.

 鴻圖圖書寒假作業假期作業吉林大學出版社系列答案
鴻圖圖書寒假作業假期作業吉林大學出版社系列答案