Question

把編號為1到6的六個小球，平均分到三個不同的盒子內．
求：（1）每盒各有一個奇數號球的概率；
（2）有一盒全是偶數號球的概率．

Answer 1

【答案】分析：根據題意，分析可得，6個球平均分入三盒有C₆²C₄²C₂²種等可能的結果，
（1）每盒各有一個奇數號球的結果有A₃³A₃³種，進而計算可得答案；
（2）有一盒全是偶數號球的結果有（C₃²C₃¹）•C₄²C₂²，進而計算可得答案．
解答：解：6個球平均分入三盒，先在第一個盒子里放兩個，有C₆²種情況，在第二個盒子里放兩個，此時剩余4個球，有C₄²種情況，最后將剩下的兩個球放入第三個盒子里，有C₂²種情況，故將6個球平均分入三盒，有C₆²C₄²C₂²種等可能的結果．
（1）由題意，先將奇數號球放進3個盒子，有A₃³種情況，再將其余的3個球放進3個盒子，有A₃³種情況，
則每盒各有一個奇數號球的結果有A₃³A₃³種，
所求概率P（A）==；
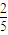
（2）由題意，先從3個偶數號球中任取2個，放進1個盒子，有（C₃²C₃¹）種情況，將剩余的4個球放進剩余的2個盒子里，有C₄²C₂²種情況，
則有一盒全是偶數號球的結果有（C₃²C₃¹）•C₄²C₂²，
所求概率P（A）==．
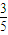
點評：本題考查組合、排列數公式的運用與等可能事件的概率，難點在于根據題意，計算每個事件的可能情況數目．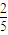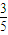