
【題目】已知數列{![]() }中,
}中, ![]() ,且
,且![]() 對任意正整數都成立,數列{
對任意正整數都成立,數列{![]() }的前n項和為Sn。
}的前n項和為Sn。
(1)若![]() ,且
,且![]() ,求a;
,求a;
(2)是否存在實數k,使數列{![]() }是公比不為1的等比數列,且任意相鄰三項
}是公比不為1的等比數列,且任意相鄰三項![]() 按某順序排列后成等差數列,若存在,求出所有k值,若不存在,請說明理由;
按某順序排列后成等差數列,若存在,求出所有k值,若不存在,請說明理由;
(3)若![]() 。
。
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
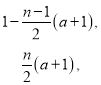
![]()
【解析】試題分析:(1)![]() 時,
時, ![]() ,由等差數列定義知數列
,由等差數列定義知數列![]() 是等差數列,由
是等差數列,由![]() 可得
可得![]() ,解得
,解得![]() ,(2)等差數列與等比數列的綜合,從等差數列列等量關系:因為數列{
,(2)等差數列與等比數列的綜合,從等差數列列等量關系:因為數列{![]() }是公比不為1,所以
}是公比不為1,所以![]() 不為等差中項,只需討論
不為等差中項,只需討論![]() 與
與![]() 為等差中項:若
為等差中項:若![]() 為等差中項,則
為等差中項,則![]() ,即
,即![]() ,化簡得:
,化簡得: ![]() ,解得
,解得![]() (舍1);
(舍1); ![]() ;同理若
;同理若![]() 為等差中項,
為等差中項, ![]() (3)
(3)![]() 則
則![]() ,
, ![]() ,從而
,從而![]() ,所以求和時要重新組合,每兩項作為一組,先求
,所以求和時要重新組合,每兩項作為一組,先求![]() 是偶數時,
是偶數時, ![]()
![]()
![]() ,再求
,再求![]() 是奇數時,
是奇數時, ![]()
![]()
![]()
![]()
![]() ,
,
試題解析:(1)![]() 時,
時, ![]() ,
, ![]() ,所以數列
,所以數列![]() 是等差數列 1分
是等差數列 1分
此時首項![]() ,公差
,公差![]() ,數列
,數列![]() 的前
的前![]() 項和是
項和是![]() 3分
3分
故![]() ,即
,即![]() ,得
,得![]() ; 4分
; 4分
(沒有過程,直接寫![]() 不給分)
不給分)
(2)設數列![]() 是等比數列,則它的公比
是等比數列,則它的公比![]() ,所以
,所以![]() ,
, ![]() ,
, ![]() 6分
6分
①若![]() 為等差中項,則
為等差中項,則![]() ,即
,即![]() ,解得:
,解得: ![]() ,不合題意;
,不合題意;
②若![]() 為等差中項,則
為等差中項,則![]() ,即
,即![]() ,化簡得:
,化簡得: ![]() ,
,
解得![]() (舍1);
(舍1); ![]() ;
;
③若![]() 為等差中項,則
為等差中項,則![]() ,即
,即![]() ,化簡得:
,化簡得: ![]() ,
,
解得![]() ;
; ![]() ; 9分
; 9分
綜上可得,滿足要求的實數![]() 有且僅有一個,
有且僅有一個, ![]() ; 10分
; 10分
(3)![]() 則
則![]() ,
,
![]() ,
, ![]() , 12分
, 12分
當![]() 是偶數時,
是偶數時,
![]()
![]()
![]() ,
,
當![]() 是奇數時,
是奇數時,
![]()
![]()
![]()
![]()
![]() ,
, ![]() 也適合上式, 15分
也適合上式, 15分
綜上可得, ![]()
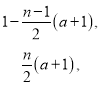
![]() . 16分
. 16分


 開心快樂假期作業暑假作業西安出版社系列答案
開心快樂假期作業暑假作業西安出版社系列答案 名題訓練系列答案
名題訓練系列答案科目:高中數學 來源: 題型:
【題目】在三棱錐P﹣ABC中,D為AB的中點.
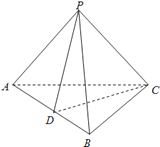
(1)與BC平行的平面PDE交AC于點E,判斷點E在AC上的位置并說明理由如下:
(2)若PA=PB,且△PCD為銳角三角形,又平面PCD⊥平面ABC,求證:AB⊥PC.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,A,B,C是橢圓M:![]() 上的三點,其中點A是橢圓的右頂點,BC過橢圓M的中心,且滿足AC⊥BC,BC=2AC。
上的三點,其中點A是橢圓的右頂點,BC過橢圓M的中心,且滿足AC⊥BC,BC=2AC。
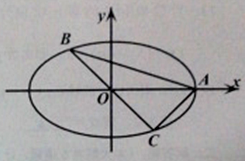
(1)求橢圓的離心率;
(2)若y軸被△ABC的外接圓所截得弦長為9,求橢圓方程。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在三棱錐P-ABC中,D為AB的中點。

(1)與BC平行的平面PDE交AC于點E,判斷點E在AC上的位置并說明理由如下:
(2)若PA=PB,且△PCD為銳角三角形,又平面PCD⊥平面ABC,求證:AB⊥PC。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本小題滿分14分)
已知拋物線![]() 的焦點為
的焦點為![]() ,
, ![]() 為
為![]() 上異于原點的任意一點,過點
上異于原點的任意一點,過點![]() 的直線
的直線![]() 交
交![]() 于另一點
于另一點![]() ,交
,交![]() 軸的正半軸于點
軸的正半軸于點![]() ,且有
,且有![]() .當點
.當點![]() 的橫坐標為
的橫坐標為![]() 時,
時, ![]() 為正三角形.
為正三角形.
(Ⅰ)求![]() 的方程;
的方程;
(Ⅱ)若直線![]() ,且
,且![]() 和
和![]() 有且只有一個公共點
有且只有一個公共點![]() ,
,
(ⅰ)證明直線![]() 過定點,并求出定點坐標;
過定點,并求出定點坐標;
(ⅱ)![]() 的面積是否存在最小值?若存在,請求出最小值;若不存在,請說明理由.
的面積是否存在最小值?若存在,請求出最小值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在某次測驗中,有6位同學的平均成績為75分.用xn表示編號為n(n=1,2,…,6)的同學所得成績,且前5位同學同學的成績如表:
n | 1 | 2 | 3 | 4 | 5 |
x0 | 70 | 76 | 72 | 70 | 72 |
(1)求第6位同學的成績x6及這6位同學成績的標準差s;
(2)若從前5位同學中,隨機地選2位同學,求恰有1位同學成績在區間[68,75)中的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市教育部門擬從18名高中數學教師中選拔2人參加省教師技能大賽.為縮短比賽時間,將這18名教師隨機分成![]() ,
, ![]() 兩組,其選拔賽成績的莖葉圖如圖所示.該教育部門先將成績不低于85分的教師初選出來進行培訓后,再從中選拔2人參加省教師技能大賽.
兩組,其選拔賽成績的莖葉圖如圖所示.該教育部門先將成績不低于85分的教師初選出來進行培訓后,再從中選拔2人參加省教師技能大賽.

(Ⅰ)若僅從初選選手中隨機抽選2人參加省賽,并記抽選的2人中來自![]() 組的人數為
組的人數為![]() ,試求
,試求![]() 的分布列和期望值;
的分布列和期望值;
(Ⅱ)在(Ⅰ)的條件下,若參加省賽的2人是同性的概率等于![]() ,求初選出來參加培訓的男教師和女教師的人數.
,求初選出來參加培訓的男教師和女教師的人數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設兩條直線的方程分別為x+y+a=0和 x+y+b=0,已知a、b是關于x的方程x2+x+c=0的兩個實根,且0≤c≤ ![]() ,則這兩條直線間距離的最大值和最小值分別為( )
,則這兩條直線間距離的最大值和最小值分別為( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com