已知點A(4,3)和圓C:(x-2)2+y2=4
(1)求圓C關于點A對稱的圓C1的標準方程;
(2)求過點A并且與圓C相切的直線方程.
【答案】
分析:(1)由題意可設,圓C關于點A對稱的圓C
1的標準方程為(x-a)
2+(y-b)
2=4則可得,(2,0)與(a,b)關于A(4,3)對稱,可求a,b
(2)設所求的切線方程為y-3=k(x-4),然后根據直線與圓相切的 性質,可知圓心(2,0)到直線kx-y+3-4k=0的距離d=2可求k,進而可求切線方程
解答:解:(1)由題意可設,圓C關于點A對稱的圓C
1的標準方程為(x-a)
2+(y-b)
2=4
則可得,(2,0)與(a,b)關于A(4,3)對稱
則
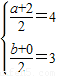
,解可得,a=6,b=6,所求的圓的方程為(x-6)
2+(y-6)
2=4
(2)設所求的切線方程為y-3=k(x-4)即kx-y+3-4k=0
由直線與圓相切的 性質,可知圓心(2,0)到直線kx-y+3-4k=0的距離d=
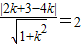
解可得,k=
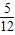
即直線方程為5x-12y+16=0
而當直線為x=4時也與圓相切,
綜上可得,所求的切線方程為5x-12y+16=0或x=4
點評:本題主要考查了兩點關于點對稱 性質的應用及直線與圓相切性質的應用,解(2)是一定要 注意有兩條切線

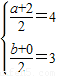 ,解可得,a=6,b=6,所求的圓的方程為(x-6)2+(y-6)2=4
,解可得,a=6,b=6,所求的圓的方程為(x-6)2+(y-6)2=4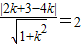
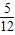 即直線方程為5x-12y+16=0
即直線方程為5x-12y+16=0

 手拉手全優練考卷系列答案
手拉手全優練考卷系列答案