若f(x)=(x-1)
4+4(x-1)
3 +6(x-1)
2 +4x-3，則f(
)的值為
A.4
B.4 C.2
D.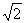
B
解析：f(x)=(x-1)4 +4(x-1)3 +6(x-1)2 +4(x-1)+1=(x-1+1)4=x4,
∴ f()=()4=4,選B.
練習冊系列答案
相關習題
科目：高中數學
來源：
題型：
設函數f（x）=a
2x
2（a＞0），g（x）=blnx．
（1）若函數y=f（x）圖象上的點到直線x-y-3=0距離的最小值為
，求a的值；
（2）關于x的不等式（x-1）
2＞f（x）的解集中的整數恰有3個，求實數a的取值范圍；
（3）對于函數f（x）與g（x）定義域上的任意實數x，若存在常數k，m，使得f（x）≥kx+m和g（x）≤kx+m都成立，則稱直線y=kx+m為函數f（x）與g（x）的“分界線”．設
a=，b=e，試探究f（x）與g（x）是否存在“分界線”？若存在，求出“分界線”的方程；若不存在，請說明理由．
查看答案和解析>>
科目：高中數學
來源：徐州模擬
題型：解答題
設函數f（x）=a
2x
2（a＞0），g（x）=blnx．
（1）若函數y=f（x）圖象上的點到直線x-y-3=0距離的最小值為
2，求a的值；
（2）關于x的不等式（x-1）
2＞f（x）的解集中的整數恰有3個，求實數a的取值范圍；
（3）對于函數f（x）與g（x）定義域上的任意實數x，若存在常數k，m，使得f（x）≥kx+m和g（x）≤kx+m都成立，則稱直線y=kx+m為函數f（x）與g（x）的“分界線”．設
a=，b=e，試探究f（x）與g（x）是否存在“分界線”？若存在，求出“分界線”的方程；若不存在，請說明理由．
查看答案和解析>>
科目：高中數學
來源：0103 期中題
題型：填空題
下列說法：
①若f(x)=ax2+（2a+b）x+2 (其中x∈[2a-1，a+4])是偶函數，則實數b=2；
②
是奇函數又是偶函數；
③已知f(x)是定義在R上的奇函數，若當x∈[0，+∞)時，f(x)=x（1+x），則當x∈R時，f(x)=x（1+|x|）；
④已知f(x)是定義在R上的不恒為零的函數，且對任意的x，y∈R都滿足f(xy)=xf(y)+yf(x)，則f(x)是奇函數；
其中所有正確說法的序號是（ ）。
查看答案和解析>>
科目：高中數學
來源：0119 期中題
題型：填空題
下列說法：①若f(x)=ax
2+（2a+b）x+2（其中x∈[2a-1，a+4]）是偶函數，則實數b=2；
②
既是奇函數又是偶函數；
③已知f(x)是定義在R上的奇函數，若當x∈[0，+∞)時，f(x)=x(1+x)，則當x∈R時，f(x)=x(1+|x|)；
④已知f(x)是定義在R上的不恒為零的函數，且對任意的x，y∈R都滿足f(x·y)=x·f(y)+y·f(x)，則f(x)是奇函數；
其中所有正確命題的序號是（ ）。
查看答案和解析>>
