
已知函數f(x)是(-∞,+∞)上的增函數,a,b∈R.
(1)若a+b≥0,求證:f(a)+f(b)≥f(-a)+f(-b);
(2)判斷(1)中命題的逆命題是否成立,并證明你的結論.
(1) 證明:∵a+b≥0,∴a≥-b. 由f(x)的單調性得f(a)≥f(-b) 又a+b≥0⇒b≥-a⇒f(b)≥f(-a) 兩式相加即得:f(a)+f(b)≥f(-a)+f(-b) (2) 逆命題成立,假設a+b<0,那么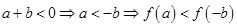 ,
,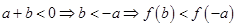 ⇒f(a)+f(b)<f(-a)+f(-b) 這與已知矛盾,故只有a+b≥0
⇒f(a)+f(b)<f(-a)+f(-b) 這與已知矛盾,故只有a+b≥0
解析試題分析:(1)證明:∵a+b≥0,∴a≥-b. 2分
由已知f(x)的單調性得f(a)≥f(-b).
又a+b≥0⇒b≥-a⇒f(b)≥f(-a). 4分
兩式相加即得:f(a)+f(b)≥f(-a)+f(-b). 6分
(2)逆命題:
f(a)+f(b)≥f(-a)+f(-b)⇒a+b≥0. 8分
下面用反證法證之.
假設a+b<0,那么: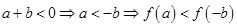
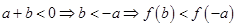
⇒f(a)+f(b)<f(-a)+f(-b). 10分
這與已知矛盾,故只有a+b≥0.逆命題得證. 12分
考點:函數單調性與反證法
點評:單調性的定義:在定義域的某個區間上,若有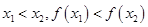 則函數為增函數,若有
則函數為增函數,若有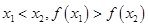 則函數為減函數;反證法證明的大體步驟:假設要證明的結論反面成立,借此推出與已知或定理發生矛盾,推翻假設肯定原結論成立
則函數為減函數;反證法證明的大體步驟:假設要證明的結論反面成立,借此推出與已知或定理發生矛盾,推翻假設肯定原結論成立


 華東師大版一課一練系列答案
華東師大版一課一練系列答案科目:高中數學 來源: 題型:解答題
定義在R上的函數f(x)是最小正周期為2的奇函數, 且當x∈(0, 1)時, f (x)=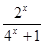 .
.
(1)求f (x)在[-1, 1]上的解析式;
(2)證明f (x)在(—1, 0)上時減函數;
(3)當λ取何值時, 不等式f (x)>λ在R上有解?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,已知正比例函數y=2x的圖像l1與反比例函數y= 的圖像相交于點A(a,2),將直線l1向上平移3個單位得到的直線l2與雙曲線相交于B、C兩點(點B在第一象限),與y軸交于點D.
的圖像相交于點A(a,2),將直線l1向上平移3個單位得到的直線l2與雙曲線相交于B、C兩點(點B在第一象限),與y軸交于點D.
(1)求反比例函數的解析式;
(2)求△DOB的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com