
【題目】設O為坐標原點,動點M在橢圓C: ![]() +y2=1上,過M做x軸的垂線,垂足為N,點P滿足
+y2=1上,過M做x軸的垂線,垂足為N,點P滿足 ![]() =
= ![]() .
.
(Ⅰ)求點P的軌跡方程;
(Ⅱ)設點Q在直線x=﹣3上,且 ![]()
![]() =1.證明:過點P且垂直于OQ的直線l過C的左焦點F.
=1.證明:過點P且垂直于OQ的直線l過C的左焦點F.
【答案】解:(Ⅰ)設M(x0 , y0),由題意可得N(x0 , 0),
設P(x,y),由點P滿足 ![]() =
= ![]() .
.
可得(x﹣x0 , y)= ![]() (0,y0),
(0,y0),
可得x﹣x0=0,y= ![]() y0 ,
y0 ,
即有x0=x,y0= ![]() ,
,
代入橢圓方程 ![]() +y2=1,可得
+y2=1,可得 ![]() +
+ ![]() =1,
=1,
即有點P的軌跡方程為圓x2+y2=2;
(Ⅱ)證明:設Q(﹣3,m),P( ![]() cosα,
cosα, ![]() sinα),(0≤α<2π),
sinα),(0≤α<2π),![]()
![]() =1,可得(
=1,可得( ![]() cosα,
cosα, ![]() sinα)(﹣3﹣
sinα)(﹣3﹣ ![]() cosα,m﹣
cosα,m﹣ ![]() sinα)=1,
sinα)=1,
即為﹣3 ![]() cosα﹣2cos2α+
cosα﹣2cos2α+ ![]() msinα﹣2sin2α=1,
msinα﹣2sin2α=1,
解得m= ![]() ,
,
即有Q(﹣3, ![]() ),
),
橢圓 ![]() +y2=1的左焦點F(﹣1,0),
+y2=1的左焦點F(﹣1,0),
由kOQ=﹣ ![]() ,
,
kPF= ![]() ,
,
由kOQkPF=﹣1,
可得過點P且垂直于OQ的直線l過C的左焦點F.
【解析】(Ⅰ)設M(x0 , y0),由題意可得N(x0 , 0),設P(x,y),運用向量的坐標運算,結合M滿足橢圓方程,化簡整理可得P的軌跡方程;
span>(Ⅱ)設Q(﹣3,m),P( ![]() cosα,
cosα, ![]() sinα),(0≤α<2π),運用向量的數(shù)量積的坐標表示,可得m,即有Q的坐標,求得橢圓的左焦點坐標,求得OQ,PF的斜率,由兩直線垂直的條件:斜率之積為﹣1,即可得證.
sinα),(0≤α<2π),運用向量的數(shù)量積的坐標表示,可得m,即有Q的坐標,求得橢圓的左焦點坐標,求得OQ,PF的斜率,由兩直線垂直的條件:斜率之積為﹣1,即可得證.
【考點精析】解答此題的關鍵在于理解斜率的計算公式的相關知識,掌握給定兩點P1(x1,y1),P2(x2,y2),x1≠x2,用兩點的坐標來表示直線P1P2的斜率:斜率公式: k=y2-y1/x2-x1,以及對兩條直線垂直與傾斜角、斜率的關系的理解,了解兩條直線都有斜率,如果它們互相垂直,那么它們的斜率互為負倒數(shù);反之,如果它們的斜率互為負倒數(shù),那么它們互相垂直.


科目:高中數(shù)學 來源: 題型:
【題目】已知海島![]() 在海島
在海島![]() 北偏東
北偏東![]() ,
,![]() ,
,![]() 相距
相距![]() 海里,物體甲從海島
海里,物體甲從海島![]() 以
以![]() 海里/小時的速度沿直線向海島
海里/小時的速度沿直線向海島![]() 移動,同時物體乙從海島
移動,同時物體乙從海島![]() 沿著海島
沿著海島![]() 北偏西
北偏西![]() 方向以
方向以![]() 海里/小時的速度移動.
海里/小時的速度移動.
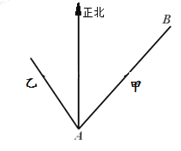
(1)問經(jīng)過多長時間,物體甲在物體乙的正東方向;
(2)求甲從海島![]() 到達海島
到達海島![]() 的過程中,甲、乙兩物體的最短距離.
的過程中,甲、乙兩物體的最短距離.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】一塊各面均涂有油漆的正方體被鋸成27個大小相同的小正方體,若將這些小正方體均勻地攪混在一起,從中任意取出一個,則取出的小正方體兩面涂有油漆的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】選修4-4:坐標系與參數(shù)方程
在平面直角坐標系![]() 中,圓
中,圓![]() 的參數(shù)方程為
的參數(shù)方程為![]() (
(![]() 為參數(shù)).在極坐標系(與平面直角坐標系
為參數(shù)).在極坐標系(與平面直角坐標系![]() 取相同的長度單位,且以原點
取相同的長度單位,且以原點![]() 為極點,以
為極點,以![]() 軸非負半軸為極軸)中,直線
軸非負半軸為極軸)中,直線![]() 的方程為
的方程為![]() .
.
(Ⅰ)求圓![]() 的普通方程及直線
的普通方程及直線![]() 的直角坐標方程;
的直角坐標方程;
(Ⅱ)設平面直角坐標系![]() 中的點
中的點![]() ,經(jīng)過點
,經(jīng)過點![]() 傾斜角為
傾斜角為![]() 的直線
的直線![]() 與
與![]() 相交于
相交于![]() ,
,![]() 兩點,求
兩點,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知關于![]() 與
與![]() 有表格中的數(shù)據(jù),且
有表格中的數(shù)據(jù),且![]() 與
與![]() 線性相關,由最小二乘法得
線性相關,由最小二乘法得![]() .
.
| 2 | 4 | 5 | 6 | 8 |
| 30 | 40 | 60 | 50 | 70 |
(1)求![]() 與
與![]() 的線性回歸方程;
的線性回歸方程;
(2)現(xiàn)有第二個線性模型:![]() ,且
,且![]() .若與(1)的線性模型比較,哪一個線性模型擬合效果比較好,請說明理由
.若與(1)的線性模型比較,哪一個線性模型擬合效果比較好,請說明理由
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,橢圓E: ![]() =1(a>b>0)的左、右焦點分別為F1 , F2 , 離心率為
=1(a>b>0)的左、右焦點分別為F1 , F2 , 離心率為 ![]() ,兩準線之間的距離為8.點P在橢圓E上,且位于第一象限,過點F1作直線PF1的垂線l1 , 過點F2作直線PF2的垂線l2 .
,兩準線之間的距離為8.點P在橢圓E上,且位于第一象限,過點F1作直線PF1的垂線l1 , 過點F2作直線PF2的垂線l2 .
(Ⅰ)求橢圓E的標準方程;
(Ⅱ)若直線l1 , l2的交點Q在橢圓E上,求點P的坐標.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】![]() 兩地相距
兩地相距![]() 千米,汽車從
千米,汽車從![]() 地勻速行駛到
地勻速行駛到![]() 地,速度不超過
地,速度不超過![]() 千米小時,已知汽車每小時的運輸成本(單位:元)由可變部分和固定部分兩部分組成:可變部分與速度
千米小時,已知汽車每小時的運輸成本(單位:元)由可變部分和固定部分兩部分組成:可變部分與速度![]() 的平方成正比,比例系數(shù)為
的平方成正比,比例系數(shù)為![]() ,固定部分為
,固定部分為![]() 元,
元,
(1)把全程運輸成本![]() (元)表示為速度
(元)表示為速度![]() (千米小時)的函效:并求出當
(千米小時)的函效:并求出當![]() 時,汽車應以多大速度行駛,才能使得全程運輸成本最小;
時,汽車應以多大速度行駛,才能使得全程運輸成本最小;
(2)隨著汽車的折舊,運輸成本會發(fā)生一些變化,那么當![]() ,此時汽車的速度應調(diào)整為多大,才會使得運輸成本最小,
,此時汽車的速度應調(diào)整為多大,才會使得運輸成本最小,
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,在平面直角坐標系![]() 中,已知圓
中,已知圓![]() :
:![]() .
.

⑴若圓![]() 的半徑為2,圓
的半徑為2,圓![]() 與
與![]() 軸相切且與圓
軸相切且與圓![]() 外切,求圓
外切,求圓![]() 的標準方程;
的標準方程;
⑵若過原點![]() 的直線
的直線![]() 與圓
與圓![]() 相交于
相交于![]() 兩點,且
兩點,且![]() ,求直線
,求直線![]() 的方程.
的方程.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com