
如圖1所示,在邊長為

的正方形

中,


,且

,

,

分別交


于點

,將該正方形沿

、

折疊,使得

與

重合,構(gòu)成如圖2所示的三棱柱

中
(Ⅰ)求證:
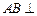

;
(Ⅱ)在底邊

上有一點

,

,
求證:

面
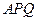
(III)求直線

與平面
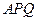
所成角的正弦值.
(Ⅰ)略,(Ⅱ)略,(Ⅲ)直線

與平面
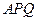
所成角的正弦值為
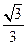
(Ⅰ)證明:因為

,

,
所以
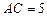
,從而
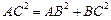
,即
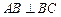
.………………………2分
又因為

,而
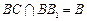
,
所以

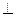
平面
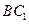
,又
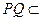
平面
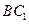
所以
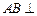

;………………4分
(Ⅱ)解:過

作
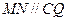
交
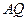
于

,連接

,
因為

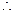
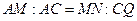
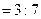
……………6分
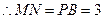
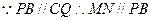
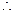
四邊形
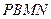
為平行四邊形
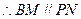
,所以

平面
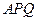
…………………………8分
(III)解:由圖1知,
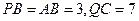
,分別以
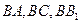
為
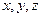
軸,
則
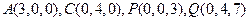
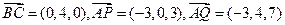
………10分
設平面
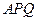
的法向量為
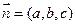
,
所以
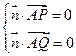
得

,
令
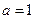
,則
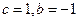
,
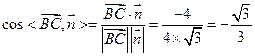
所以直線

與平面
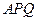
所成角的正弦值為
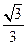
…………………………12分
練習冊系列答案
相關習題
科目:高中數(shù)學
來源:不詳
題型:填空題
已知正方體ABCD-A1B1C1D1的棱長為2,點E為棱AB的中點。求:D1E與平面BC1D所成角的大小(用余弦值表示)
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
設△
ABC和△
DBC所在的兩個平面互相垂直,且
AB=
BC=
BD,∠
ABC=∠
DBC=

,求:
(1)直線
AD與平面
BCD所成角的大小;
(2)異面直線
AD與
BC所成的角;
(3)二面角
A—
BD—
C的大小.

查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
設直線

平面

,過平面

外一點

與

都成

角

的直線有且
只有 ( )
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
如圖,正方體ABCD-A
1B
1C
1D
1的棱長為1,點M在A上,且AM=

AB,點P在平面ABCD上,且動點P到直線A
1D
1的距離的平方與P到點M的距離的平方差為1,在平面直角坐標系xAy中,動點P的軌跡方程是
.

查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
三棱錐A-BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,點E、F分別在AC,AD上,使平面BEF⊥平面ACD,且EF∥CD,則平面BEF與平面BCD所成的二面角的正弦值為 ( )
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
如圖,正三棱柱ABC-A
1B
1C
1的底面邊長為1,高為h(h>3),點M在側(cè)棱BB
1上移動,并且M到底面ABC的距離為x,且AM與側(cè)面BCC
1B
1所成的角為α.
(1)若α在區(qū)間
[,]上變化,求x的變化范圍;
(2)若α為
,求AM與BC所成角的余弦值.

查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
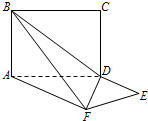
如圖,平面ABCD⊥平面ADEF,其中ABCD為矩形,ADEF為梯形,AF
∥DE,AF⊥FE,AF=AD=2DE=2.
(Ⅰ)求異面直線EF與BC所成角的大小;
(Ⅱ)若二面角A-BF-D的平面角的余弦值為
,求AB的長.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
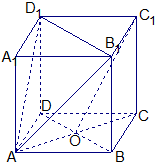
已知正方體ABCD-A
1B
1C
1D
1,O是底ABCD對角線的交點.
(1)求證:C
1O
∥面AB
1D
1;
(2)求異面直線AD
1與C
1O所成角的大小.
查看答案和解析>>

 如圖1所示,在邊長為
如圖1所示,在邊長為 的正方形
的正方形 中,
中,
 ,且
,且 ,
, ,
, 分別交
分別交
 于點
于點 ,將該正方形沿
,將該正方形沿 、
、 折疊,使得
折疊,使得 與
與 重合,構(gòu)成如圖2所示的三棱柱
重合,構(gòu)成如圖2所示的三棱柱 中
中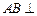
 ;
; 上有一點
上有一點 ,
, ,
, 面
面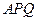
 與平面
與平面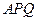 所成角的正弦值.
所成角的正弦值. 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案 ,求:
,求: 
 AB,點P在平面ABCD上,且動點P到直線A1D1的距離的平方與P到點M的距離的平方差為1,在平面直角坐標系xAy中,動點P的軌跡方程是 .
AB,點P在平面ABCD上,且動點P到直線A1D1的距離的平方與P到點M的距離的平方差為1,在平面直角坐標系xAy中,動點P的軌跡方程是 . 






