
【題目】如圖,在平面直角坐標系中,點A![]() ,B
,B![]() ,銳角α的終邊與單位圓O交于點P.
,銳角α的終邊與單位圓O交于點P.
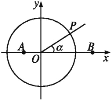
(1)用α的三角函數表示點P的坐標;
(2)當![]() =-
=-![]() 時,求α的值;
時,求α的值;
(3)在x軸上是否存在定點M,使得|![]() |=
|=![]() |恒成立?若存在,求出點M的坐標;若不存在,請說明理由.
|恒成立?若存在,求出點M的坐標;若不存在,請說明理由.
【答案】(1)(cos α,sin α);(2)α=60°;(3)M(-2,0).
【解析】
![]() 用
用![]() 的三角函數的坐標法定義得到答案
的三角函數的坐標法定義得到答案
![]() 首先寫出兩個向量的坐標,根據
首先寫出兩個向量的坐標,根據![]() ,整理計算即可求出
,整理計算即可求出![]() 的值
的值
![]() 假設存在定點
假設存在定點![]() ,進行向量的模長運算,求得恒成立時的
,進行向量的模長運算,求得恒成立時的![]() 值
值
(1)用α的三角函數表示點P的坐標為(cos α,sin α).
(2)![]() ,
,
![]() =-
=-![]() 時,
時,
即![]() +sin2α=-
+sin2α=-![]() ,
,
整理得到cos α=![]() ,所以銳角α=60°.
,所以銳角α=60°.
(3)在x軸上假設存在定點M,設M(x,0),![]() =(cos α-x,sin α),
=(cos α-x,sin α),
則由|![]() |=
|=![]() |恒成立,得到
|恒成立,得到![]() +cos α=
+cos α=![]() (1-2xcos α+x2),整理得2(2+x)cos α=x2-4,
(1-2xcos α+x2),整理得2(2+x)cos α=x2-4,
當x=-2時等式恒成立,所以存在M(-2,0).


 探究與鞏固河南科學技術出版社系列答案
探究與鞏固河南科學技術出版社系列答案科目:高中數學 來源: 題型:
【題目】某省組織了一次高考模擬考試,該省教育部門抽取了1000名考生的數學考試成績,并繪制成頻率分布直方圖如圖所示. 
(Ⅰ)求樣本中數學成績在95分以上(含95分)的學生人數;
(Ⅱ)已知本次模擬考試全省考生的數學成績X~N(μ,σ2),其中μ近似為樣本的平均數,σ2近似為樣本方差,試估計該省的所有考生中數學成績介于100~138.2分的概率;
(Ⅲ)以頻率估計概率,若從該省所有考生中隨機抽取4人,記這4人中成績在[105,125)內的人數為X,求X的分布列及數學期望.
參考數據: ![]() ≈18.9,
≈18.9, ![]() ≈19.1,
≈19.1, ![]() ≈19.4.
≈19.4.
若Z∽N(μ,σ2),則P(μ﹣σ<Z<μ+σ)=0.9826,P(μ﹣2σ<Z<μ+2σ)=0.9544,P(μ﹣3σ<Z<μ+3σ)=0.9976.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】α、β是兩個平面,m、n是兩條直線,有下列四個命題:
①如果m⊥n , m⊥α , n∥β , 那么α⊥β.
②如果m⊥α , n∥α , 那么m⊥n.
③如果α∥β , m ![]() α , 那么m∥β.
α , 那么m∥β.
④如果m∥n , α∥β , 那么m與α所成的角和n與β所成的角相等.
其中正確的命題有.(填寫所有正確命題的編號)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖1,在長方形![]() 中,
中,![]() 為
為![]() 的中點,
的中點,![]() 為線段
為線段![]() 上一動點.現將
上一動點.現將![]() 沿
沿![]() 折起,形成四棱錐
折起,形成四棱錐![]() .
.



圖1 圖2 圖3
(Ⅰ)若![]() 與
與![]() 重合,且
重合,且![]() (如圖2).
(如圖2).
(ⅰ)證明:![]() 平面
平面![]() ;
;
(ⅱ)求二面角![]() 的余弦值.
的余弦值.
(Ⅱ)若![]() 不與
不與![]() 重合,且平面
重合,且平面![]() 平面
平面![]() (如圖3),設
(如圖3),設![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】將函數 ![]() 圖像上的點P(
圖像上的點P( ![]() ,t )向左平移s(s﹥0) 個單位長度得到點P′.若 P′位于函數y=sin2x的圖像上,則( )
,t )向左平移s(s﹥0) 個單位長度得到點P′.若 P′位于函數y=sin2x的圖像上,則( )
A.t= ![]() ,s的最小值為
,s的最小值為 ![]()
B.t= ![]() ,s的最小值為
,s的最小值為 ![]()
C.t= ![]() ,s的最小值為
,s的最小值為 ![]()
D.t= ![]() ,s的最小值為
,s的最小值為 ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】從含有兩件正品a,b和一件次品c的3件產品中每次任取一件,連續取兩次,求取出的兩件產品中,恰有一件是次品的概率。
(1)每次取出不放回;(2)每次取出放回;
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ax+bx(a>0,b>0,a≠1,b≠1).
(1)設a=2,b= ![]() .
.
①求方程f(x)=2的根;
②若對于任意x∈R,不等式f(2x)≥mf(x)﹣6恒成立,求實數m的最大值;
(2)若0<a<1,b>1,函數g(x)=f(x)﹣2有且只有1個零點,求ab的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
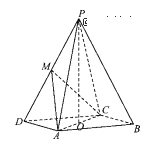
【題目】在四棱錐P-ABC中,底面ABCD為平行四邊形,![]() ,O為AC的中點,
,O為AC的中點,![]() 平面
平面![]() M為PD的中點。
M為PD的中點。
(1)證明![]() 平面
平面![]() .
.
(2)證明![]() 平面
平面![]() .
.
(3)求三棱錐P-MAC體積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com