
已知函數 (
( ,c是實數常數)的圖像上的一個最高點
,c是實數常數)的圖像上的一個最高點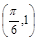 ,與該最高點最近的一個最低點是
,與該最高點最近的一個最低點是 ,
,
(1)求函數 的解析式及其單調增區間;
的解析式及其單調增區間;
(2)在△ABC中,角A、B、C所對的邊分別為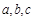 ,且
,且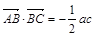 ,角A的取值范圍是區間M,當
,角A的取值范圍是區間M,當 時,試求函數
時,試求函數 的取值范圍.
的取值范圍.
(1) ,單調遞增區間是
,單調遞增區間是 ;(2)
;(2) .
.
【解析】
試題分析:(1)三角函數問題一般都要化為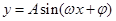
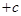 的一個三角函數的形式,然后才可利用正弦函數的性質解題,這個函數圖象上相鄰有最高點與最低點的橫坐標之差的絕對值為半個周期,而周期
的一個三角函數的形式,然后才可利用正弦函數的性質解題,這個函數圖象上相鄰有最高點與最低點的橫坐標之差的絕對值為半個周期,而周期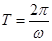 ,再加上最高(低)點在函數圖象上,我們就可出這個函數的解析式了(
,再加上最高(低)點在函數圖象上,我們就可出這個函數的解析式了(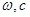 );(2)由
);(2)由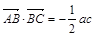 ,根據向量數量積定義我們可求出
,根據向量數量積定義我們可求出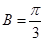 ,那么三角形的另一內角
,那么三角形的另一內角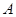 的范圍應該是
的范圍應該是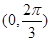 ,即函數
,即函數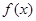 中
中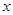 的范圍是
的范圍是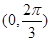 ,然后我們把
,然后我們把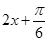 一個整體,得出
一個整體,得出 ,而正弦函數
,而正弦函數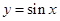 在
在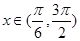 時取值范圍是
時取值范圍是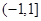 ,因此可求出
,因此可求出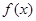 的值域.
的值域.
試題解析:(1)∵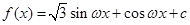 ,
,
∴ .
.
∵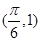 和
和 分別是函數圖像上相鄰的最高點和最低點,
分別是函數圖像上相鄰的最高點和最低點,
∴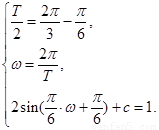 解得
解得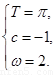
∴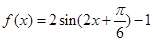 .
.
由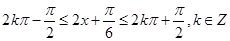 ,解得
,解得 .
.
∴函數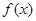 的單調遞增區間是
的單調遞增區間是 .
.
(2)∵在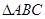 中,
中,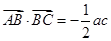 ,
,
∴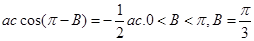 .
.
∴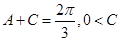 ,即
,即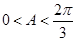 .
.
∴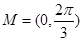 .
.
當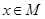 時,
時, ,考察正弦函數
,考察正弦函數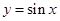 的圖像,可知,
的圖像,可知,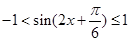 .
.
∴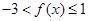 ,即函數
,即函數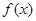 的取值范圍是
的取值范圍是 .
.
考點:(1)五點法與函數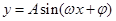
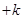 的圖象;(2)三角函數在給定區間的值域.
的圖象;(2)三角函數在給定區間的值域.


科目:高中數學 來源:2006-2007年福建泉州一中、五中、七中高三聯考數學試題 題型:044
(文)已知函數![]() ,其中C是實數,
,其中C是實數,
(Ⅰ)求f(x)的極大值和極小值;
(Ⅱ)證明方程f(x)=0的不同實根的個數不大于3.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年上海黃浦區高三上學期期末考試(即一模)理數學卷(解析版) 題型:解答題
已知函數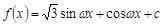 (
(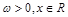 ,c是實數常數)的圖像上的一個最高點
,c是實數常數)的圖像上的一個最高點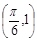 ,與該最高點最近的一個最低點是
,與該最高點最近的一個最低點是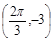 ,
,
(1)求函數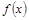 的解析式及其單調增區間;
的解析式及其單調增區間;
(2)在△ABC中,角A、B、C所對的邊分別為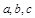 ,且
,且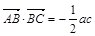 ,角A的取值范圍是區間M,當
,角A的取值范圍是區間M,當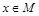 時,試求函數
時,試求函數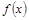 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年吉林通化第一中學高三上學期第二次月考理科數學試卷(解析版) 題型:選擇題
已知函數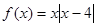
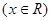 ,若存在正實數
,若存在正實數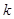 ,使得方程
,使得方程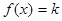 有兩個根
有兩個根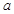 ,
,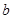 ,其中
,其中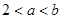 ,則
,則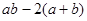 的取值范圍是( )
的取值范圍是( )
A.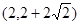 B.
B.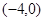 C.
C.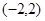 D.
D.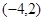
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com