
【題目】已知數列![]() ,其前
,其前![]() 項和為
項和為![]() .
.
(1)若對任意的![]() ,
, ![]() ,
, ![]() ,
, ![]() 組成公差為4的等差數列,且
組成公差為4的等差數列,且![]() ,求
,求![]() ;
;
(2)若數列 是公比為
是公比為![]() (
(![]() )的等比數列,
)的等比數列, ![]() 為常數,
為常數,
求證:數列![]() 為等比數列的充要條件為
為等比數列的充要條件為![]() .
.
【答案】(1)![]() ;(2)證明見解析.
;(2)證明見解析.
【解析】試題分析:(1)根據題意,可求得![]() ,
, ![]() (
(![]() ),從而得
),從而得![]() ,
, ![]() ,
, ![]() ,……,
,……, ![]() ,
, ![]() 是公差為4的等差數列,且
是公差為4的等差數列,且![]() ,于是可求
,于是可求![]() ;
;
(2)由![]() ,可求得
,可求得![]() ,
,![]() ,兩式相減得
,兩式相減得![]() ,若
,若![]() ,可證得數列
,可證得數列![]() 為等比數列,(充分性);若數列
為等比數列,(充分性);若數列![]() 為等比數列,可證得
為等比數列,可證得![]() ,(必要性).
,(必要性).
試題解析:(1)因為![]() ,
, ![]() ,
, ![]() 成公差為4的等差數列,
成公差為4的等差數列,
所以![]() ,
, ![]() (
(![]() ),
),
所以![]() ,
, ![]() ,
, ![]() ,……,
,……, ![]() ,
, ![]() 是公差為4的等差數列,且
是公差為4的等差數列,且
![]() ,
,
又因為![]() ,所以
,所以![]()
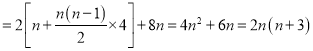
(2)因為![]() ,所以
,所以![]() ,①
,①
所以![]() ,②
,②
②-①,得![]() ,③
,③
(i)充分性:因為![]() ,所以
,所以![]() ,
, ![]() ,
, ![]() ,代入③式,得
,代入③式,得
![]() ,因為
,因為![]() ,又
,又![]() ,
,
所以![]() ,
, ![]() ,所以
,所以![]() 為等比數列,
為等比數列,
(ii)必要性:設![]() 的公比為
的公比為![]() ,則由③得
,則由③得![]() ,
,
整理得![]() ,
,
此式為關于![]() 的恒等式,若
的恒等式,若![]() ,則左邊=0,右邊=-1,矛盾:
,則左邊=0,右邊=-1,矛盾:
若![]() ,當且僅當
,當且僅當 時成立,所以
時成立,所以![]() .
.
由(i)、(ii)可知,數列![]() 為等比數列的充要條件
為等比數列的充要條件![]() .
.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:高中數學 來源: 題型:
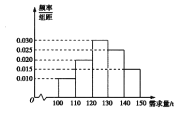
【題目】經銷商經銷某種農產品,在一個銷售季度內,每售出![]() 該產品獲利潤500元,未售出的產品,每
該產品獲利潤500元,未售出的產品,每![]() 虧損300元.根據歷史資料,得到銷售季度內市場需求量的頻率分布直方圖,如圖所示.經銷商為下一個銷售季度購進了
虧損300元.根據歷史資料,得到銷售季度內市場需求量的頻率分布直方圖,如圖所示.經銷商為下一個銷售季度購進了![]() 該農產品.以
該農產品.以![]() (單位:
(單位: ![]() )表示下一個銷售季度內的市場需求量,
)表示下一個銷售季度內的市場需求量, ![]() (單位:元)表示下一個銷售季度內經銷該農產品的利潤.
(單位:元)表示下一個銷售季度內經銷該農產品的利潤.
(1)將![]() 表示為
表示為![]() 的函數;
的函數;
(2)根據直方圖估計利潤![]() 不少于57000元的概率;
不少于57000元的概率;
(3)在直方圖的需求量分組中,以各組的區間中點值代表該組的各個值,并以需求量落入該區間的頻率作為需求量取該區間中點值的概率(例如:若需求量![]() ,則取
,則取![]() ,且
,且![]() 的概率等于需求量落入
的概率等于需求量落入![]() 的頻率),求
的頻率),求![]() 的數學期望.
的數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“微信運動”已成為當下熱門的運動方式,小王的微信朋友圈內也有大量好友參與了“微信運動”,他隨機選取了其中的40人(男、女各20人),記錄了他們某一天的走路步數,并將數據整理如下:
步數 性別 | 0-2000 | 2001-5000 | 5001-8000 | 8001-10000 | >10000 |
男 | 1 | 2 | 3 | 6 | 8 |
女 | 0 | 2 | 10 | 6 | 2 |
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
附: 
(1)已知某人一天的走路步數超過8000步被系統評定為“積極型”,否則為“懈怠型”,根據題意完成下面的 積極型 懈怠型 總計 男 女 總計 (2)若小王以這40位好友該日走路步數的頻率分布來估計其所有微信好友每日走路步數的概率分布,現從小王的所有微信好友中任選2人,其中每日走路不超過5000步的有![]() 列聯表,并據此判斷能否有95%以上的把握認為“評定類型”與“性別”有關?
列聯表,并據此判斷能否有95%以上的把握認為“評定類型”與“性別”有關?![]() 人,超過10000步的有
人,超過10000步的有![]() 人,設
人,設![]() ,求
,求![]() 的分布列及數學期望.
的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() ,其前
,其前![]() 項和為
項和為![]() .
.
(1)若對任意的![]() ,
, ![]() ,
, ![]() ,
, ![]() 組成公差為4的等差數列,且
組成公差為4的等差數列,且![]() ,求
,求![]() ;
;
(2)若數列 是公比為
是公比為![]() (
(![]() )的等比數列,
)的等比數列, ![]() 為常數,
為常數,
求證:數列![]() 為等比數列的充要條件為
為等比數列的充要條件為![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙等五名奧運志愿者被隨機地分到A,B,C,D四個不同的崗位服務,每個崗位至少有一名志愿者.
(1)求甲、乙兩人同時參加A崗位服務的概率;
(2)求甲、乙兩人不在同一個崗位服務的概率;
(3)設隨機變量ξ為這五名志愿者中參加A崗位服務的人數,求ξ的分布列.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了了解小學生的體能情況,抽取了某校一個年級的部分學生進行一分鐘跳繩次數測試,將所得數據整理后,畫出頻率分布直方圖(如圖),已知圖中從左到右前三個小組的頻率分別為 0.1,0.3,0.4,第一小組的頻數為 5. 
(1)求第四小組的頻率;
(2)若次數在 75 次以上(含75 次)為達標,試估計該年級學生跳繩測試的達標率.
(3)在這次測試中,一分鐘跳繩次數的中位數落在哪個小組內?試求出中位數.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com