
【題目】在正四面體ABCD中,點E,F分別是AB,BC的中點,則下列命題正確的序號是______
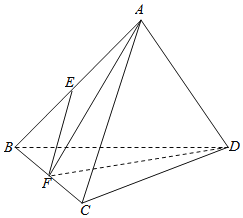
①異面直線AB與CD所成角為90°;
②直線AB與平面BCD所成角為60°;
③直線EF∥平面ACD
④平面AFD⊥平面BCD.
【答案】①③④
【解析】
在①中,由AB⊥平面CDE,知異面直線AB與CD所成角為90°;在②中,直線AB與平面BCD所成角為![]() ;在③中由EF∥AC,知直線EF∥平面ACD;在④中,由BC⊥平面ADF,知平面AFD⊥平面BCD,從而得到結果
;在③中由EF∥AC,知直線EF∥平面ACD;在④中,由BC⊥平面ADF,知平面AFD⊥平面BCD,從而得到結果
解:正四面體ABCD中,點E,F分別是AB,BC的中點,
在①中,∵正四面體ABCD中,點E、F分別是AB,BC的中點,
∴CE⊥AB,DE⊥AB,
又![]() ,∴AB⊥平面CDE,
,∴AB⊥平面CDE,
∵CD平面CDE,
∴![]() ,即異面直線AB與CD所成角為90°,故①正確;
,即異面直線AB與CD所成角為90°,故①正確;
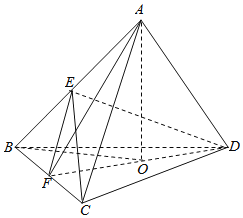
在②中,過A作AO⊥平面BCD,交DF=O,連結BO,
則∠ABO是直線AB與平面BCD所成角,
設正四面體ABCD的棱長為2,
則DF=![]() ,BO=
,BO=![]() ,
,
cos![]() =
=![]() =
=![]()
∴直線AB與平面BCD所成角為![]() ,故②錯誤;
,故②錯誤;
在③中,∵點E、F分別是AB,BC的中點,
∴EF∥AC,
∵EF![]() 平面ACD,AC平面ACD,
平面ACD,AC平面ACD,
∴直線EF∥平面ACD,故③正確;
在④中,由AF⊥BC,DF⊥BC,
又![]() ,∴BC⊥平面ADF,
,∴BC⊥平面ADF,
∵BC平面BCD,∴平面AFD⊥平面BCD,故④正確
故答案為:①③④


科目:高中數學 來源: 題型:
【題目】已知函數![]() ,其中
,其中![]() .
.![]() 是自然對數的底數.
是自然對數的底數.
(1)若曲線![]() 在
在![]() 處的切線方程為
處的切線方程為![]() .求實數
.求實數![]() 的值;
的值;
(2)① 若![]() 時,函數
時,函數![]() 既有極大值,又有極小值,求實數
既有極大值,又有極小值,求實數![]() 的取值范圍;
的取值范圍;
② 若![]() ,
,![]() .若
.若![]() 對一切正實數
對一切正實數![]() 恒成立,求實數
恒成立,求實數![]() 的最大值(用
的最大值(用![]() 表示).
表示).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知無窮數列{an}(an∈Z)的前n項和為Sn,記S1,S2,…,Sn中奇數的個數為bn.
(1)若an=n,請寫出數列{bn}的前5項;
(2)求證:“a1為奇數,ai(i=2,3,4,…)為偶數”是“數列{bn}是單調遞增數列”的充分不必要條件;
(3)若ai=bi,i=1,2,3,…,求數列{an}的通項公式.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列結論中正確的是( )
A.以直角三角形的一邊所在直線為旋轉軸,其余各邊旋轉一周而形成的面所圍成的幾何體是一個圓錐
B.以直角梯形的一邊所在直線為旋轉軸,其余各邊旋轉一周而形成的面所圍成的幾何體是一個圓臺
C.以平行四邊形的一邊所在直線為旋轉軸,其余各邊旋轉一周而形成的面所圍成的幾何體是一個圓柱
D.圓面繞其一條直徑所在直線旋轉![]() 后得到的幾何體是一個球
后得到的幾何體是一個球
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com