
已知函數(shù)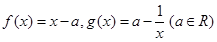 .
.
(1)判斷函數(shù) 在
在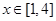 的單調性并用定義證明;
的單調性并用定義證明;
(2)令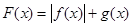 ,求
,求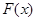 在區(qū)間
在區(qū)間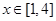 的最大值的表達式
的最大值的表達式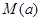 .
.
(1)函數(shù)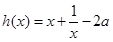 在
在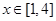 遞增;證明詳見答案解析.
遞增;證明詳見答案解析.
(2)當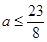 時,
時,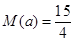 ;當
;當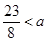 時,
時,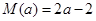 .
.
解析試題分析:(1)先根據(jù)已知條件求出 ,再根據(jù)單調性的定義證明即可;
,再根據(jù)單調性的定義證明即可;
(2)由(1)先求出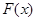 的表達式,再根據(jù)單調性求得各個區(qū)間的最大值,綜上即可求出
的表達式,再根據(jù)單調性求得各個區(qū)間的最大值,綜上即可求出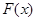 在區(qū)間
在區(qū)間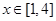 的最大值的表達式
的最大值的表達式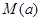 .
.
試題解析:(1)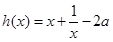 在
在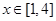 遞增;
遞增;
證明如下:
在區(qū)間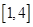 上任取
上任取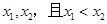
則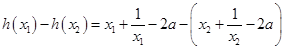

而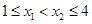 ,所以
,所以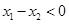 ,
,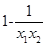 >0
>0
所以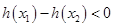 ,即函數(shù)
,即函數(shù) 在
在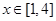 的單調遞增;(6分)
的單調遞增;(6分)
(2)若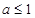 ,
,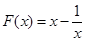 ,在
,在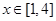 遞增,
遞增,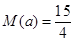 ,
,
若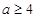 ,
,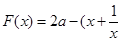 )在
)在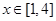 遞減,
遞減,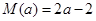 , (9分)
, (9分)
若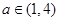 ,則
,則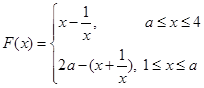 (11分)
(11分)
當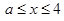 時,函數(shù)遞增,
時,函數(shù)遞增,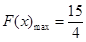 ,
,
當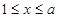 時,函數(shù)遞減,
時,函數(shù)遞減,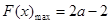 ; (13分)
; (13分)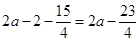 ,當
,當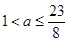 時,
時,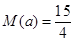 ,當
,當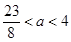 時,
時,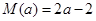 .
.
綜上: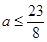 時,
時,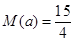 ,當
,當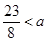 時,
時,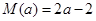 . (15分)
. (15分)
考點:函數(shù)的單調性、分段函數(shù)求值域問題.


科目:高中數(shù)學 來源: 題型:解答題
某單位擬建一個扇環(huán)面形狀的花壇(如圖所示),該扇環(huán)面是由以點 為圓心的兩個同心圓弧和延長后通過點
為圓心的兩個同心圓弧和延長后通過點 的兩條直線段圍成.按設計要求扇環(huán)面的周長為30米,其中大圓弧所在圓的半徑為10米.設小圓弧所在圓的半徑為
的兩條直線段圍成.按設計要求扇環(huán)面的周長為30米,其中大圓弧所在圓的半徑為10米.設小圓弧所在圓的半徑為 米,圓心角為
米,圓心角為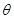 (弧度).
(弧度).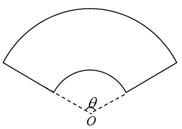
(1)求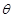 關于
關于 的函數(shù)關系式;
的函數(shù)關系式;
(2)已知在花壇的邊緣(實線部分)進行裝飾時,直線部分的裝飾費用為4元/米,弧線部分的裝飾費用為9元/米.設花壇的面積與裝飾總費用的比為 ,求
,求 關于
關于 的函數(shù)關系式,并求出
的函數(shù)關系式,并求出 為何值時,
為何值時, 取得最大值?
取得最大值?
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
設函數(shù)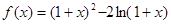
(1)若關于x的不等式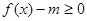 在
在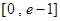 有實數(shù)解,求實數(shù)m的取值范圍;
有實數(shù)解,求實數(shù)m的取值范圍;
(2)設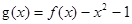 ,若關于x的方程
,若關于x的方程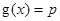 至少有一個解,求p的最小值.
至少有一個解,求p的最小值.
(3)證明不等式: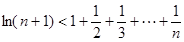
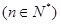
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
我國加入WTO后,根據(jù)達成的協(xié)議,若干年內某產品關稅與市場供應量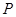 的關系允許近似的滿足:
的關系允許近似的滿足: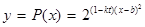 (其中
(其中 為關稅的稅率,且
為關稅的稅率,且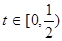 ,
, 為市場價格,
為市場價格,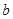 、
、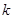 為正常數(shù)),當
為正常數(shù)),當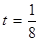 時的市場供應量曲線如圖:
時的市場供應量曲線如圖: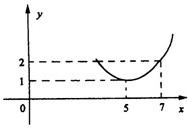
(1)根據(jù)圖象求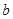 、
、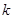 的值;
的值;
(2)若市場需求量為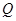 ,它近似滿足
,它近似滿足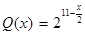 .當
.當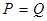 時的市場價格稱為市場平衡價格.為使市場平衡價格控制在不低于9元,求稅率
時的市場價格稱為市場平衡價格.為使市場平衡價格控制在不低于9元,求稅率 的最小值.
的最小值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
某單位擬建一個扇環(huán)面形狀的花壇(如圖所示),該扇環(huán)面是由以點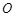 為圓心的兩個同心圓弧和延長后通過點
為圓心的兩個同心圓弧和延長后通過點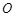 的兩條直線段圍成.按設計要求扇環(huán)面的周長為30米,其中大圓弧所在圓的半徑為10米.設小圓弧所在圓的半徑為
的兩條直線段圍成.按設計要求扇環(huán)面的周長為30米,其中大圓弧所在圓的半徑為10米.設小圓弧所在圓的半徑為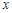 米,圓心角為
米,圓心角為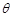 (弧度).
(弧度).
(1)求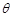 關于
關于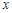 的函數(shù)關系式;
的函數(shù)關系式;
(2)已知在花壇的邊緣(實線部分)進行裝飾時,直線部分的裝飾費用為4元/米,弧線部分的裝飾費用為9元/米.設花壇的面積與裝飾總費用的比為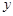 ,求
,求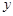 關于
關于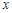 的函數(shù)關系式,并求出
的函數(shù)關系式,并求出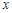 為何值時,
為何值時,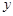 取得最大值?
取得最大值?
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
已知函數(shù)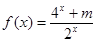 是奇函數(shù).
是奇函數(shù).
(1)求m的值:
(2)設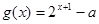 .若函數(shù)
.若函數(shù) 與
與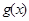 的圖象至少有一個公共點.求實數(shù)a的取值范圍.
的圖象至少有一個公共點.求實數(shù)a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
如果函數(shù) 滿足在集合
滿足在集合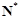 上的值域仍是集合
上的值域仍是集合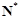 ,則把函數(shù)
,則把函數(shù) 稱為N函數(shù).
稱為N函數(shù).
例如: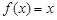 就是N函數(shù).
就是N函數(shù).
(Ⅰ)判斷下列函數(shù):①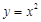 ,②
,②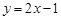 ,③
,③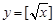 中,哪些是N函數(shù)?(只需寫出判斷結果);
中,哪些是N函數(shù)?(只需寫出判斷結果);
(Ⅱ)判斷函數(shù)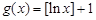 是否為N函數(shù),并證明你的結論;
是否為N函數(shù),并證明你的結論;
(Ⅲ)證明:對于任意實數(shù)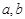 ,函數(shù)
,函數(shù)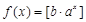 都不是N函數(shù).
都不是N函數(shù).
(注:“ ”表示不超過
”表示不超過 的最大整數(shù))
的最大整數(shù))
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com