
【題目】某公司為確定下一年度投入某種產品的宣傳費,需了解年宣傳費對年銷售量(單位:t)的影響.該公司對近5年的年宣傳費和年銷售量數據進行了研究,發現年宣傳費x(萬元)和年銷售量y(單位:t)具有線性相關關系,并對數據作了初步處理,得到下面的一些統計量的值.

(1)根據表中數據建立年銷售量y關于年宣傳費x的回歸方程;
(2)已知這種產品的年利潤z與x,y的關系為![]() ,根據(1)中的結果回答下列問題:
,根據(1)中的結果回答下列問題:
①當年宣傳費為10萬元時,年銷售量及年利潤的預報值是多少?
②估算該公司應該投入多少宣傳費,才能使得年利潤與年宣傳費的比值最大.
附:回歸方程![]() 中的斜率和截距的最小二乘估計公式分別為
中的斜率和截距的最小二乘估計公式分別為

參考數據:![]() .
.
 浙大優學小學年級銜接捷徑浙江大學出版社系列答案
浙大優學小學年級銜接捷徑浙江大學出版社系列答案科目:高中數學 來源: 題型:
【題目】已知函數![]() 圖象相鄰兩條對稱軸的距離為
圖象相鄰兩條對稱軸的距離為![]() ,將函數
,將函數![]() 的圖象向左平移
的圖象向左平移![]() 個單位后,得到的圖象關于y軸對稱則函數
個單位后,得到的圖象關于y軸對稱則函數![]() 的圖象( )
的圖象( )
A. 關于直線![]() 對稱 B. 關于直線
對稱 B. 關于直線![]() 對稱
對稱
C. 關于點![]() 對稱 D. 關于點
對稱 D. 關于點![]() 對稱
對稱
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C:![]() 的離心率
的離心率![]() ,連接橢圓的四個頂點得到的菱形的面積為
,連接橢圓的四個頂點得到的菱形的面積為![]() .
.

![]() 求橢圓C的方程;
求橢圓C的方程;
![]() 如圖所示,該橢圓C的左、右焦點
如圖所示,該橢圓C的左、右焦點![]() ,
,![]() 作兩條平行的直線分別交橢圓于A,B,C,D四個點,試求平行四邊形ABCD面積的最大值.
作兩條平行的直線分別交橢圓于A,B,C,D四個點,試求平行四邊形ABCD面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國是世界上嚴重缺水的國家,某市為了制定合理的節水方案,對居民用水情況進行調查,通過抽樣,獲得某年100為居民每人的月均用水量(單位:噸),將數據按照![]() 分成9組,制成了如圖所示的頻率分布直方圖.
分成9組,制成了如圖所示的頻率分布直方圖.
(1)求直方圖的![]() 的值;
的值;
(2)設該市有30萬居民,估計全市居民中月均用水量不低于3噸的人數,說明理由.
(3)估計居民月用水量的中位數.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某蔬果經銷商銷售某種蔬果,售價為每公斤25元,成本為每公斤15元.銷售宗旨是當天進貨當天銷售.如果當天賣不出去,未售出的全部降價以每公斤10元處理完.根據以往的銷售情況,得到如圖所示的頻率分布直方圖:

(1)根據頻率分布直方圖計算該種蔬果日需求量的平均數![]() (同一組中的數據用該組區間中點值代表);
(同一組中的數據用該組區間中點值代表);
(2)該經銷商某天購進了250公斤這種蔬果,假設當天的需求量為![]() 公斤
公斤![]() ,利潤為
,利潤為![]() 元.求
元.求![]() 關于
關于![]() 的函數關系式,并結合頻率分布直方圖估計利潤
的函數關系式,并結合頻率分布直方圖估計利潤![]() 不小于1750元的概率.
不小于1750元的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】天壇公園是明、清兩代皇帝“祭天”“祈谷”的場所.天壇公園中的圜丘臺共有三層(如圖1所示),上層壇的中心是一塊呈圓形的大理石板,從中心向外圍以扇面形石(如圖2所示).上層壇從第一環至第九環共有九環,中層壇從第十環至第十八環共有九環,下層壇從第十九環至第二十七環共有九環;第一環的扇面形石有9塊,從第二環起,每環的扇面形石塊數比前一環多9塊,則第二十七環的扇面形石塊數是______;上、中、下三層壇所有的扇面形石塊數是_______.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】現有一長為100碼,寬為80碼,球門寬為8碼的矩形足球運動場地,如圖所示,其中![]() 是足球場地邊線所在的直線,球門
是足球場地邊線所在的直線,球門![]() 處于所在直線的正中間位置,足球運動員(將其看做點
處于所在直線的正中間位置,足球運動員(將其看做點![]() )在運動場上觀察球門的角
)在運動場上觀察球門的角![]() 稱為視角.
稱為視角.
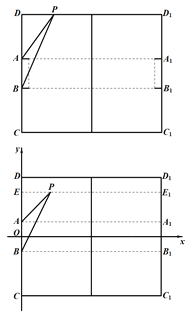
(1)當運動員帶球沿著邊線![]() 奔跑時,設
奔跑時,設![]() 到底線的距離為
到底線的距離為![]() 碼,試求當
碼,試求當![]() 為何值時
為何值時![]() 最大;
最大;
(2)理論研究和實踐經驗表明:張角![]() 越大,射門命中率就越大.現假定運動員在球場都是沿著垂直于底線的方向向底線運球,運動到視角最大的位置即為最佳射門點,以
越大,射門命中率就越大.現假定運動員在球場都是沿著垂直于底線的方向向底線運球,運動到視角最大的位置即為最佳射門點,以![]() 的中點為原點建立如圖所示的直角坐標系,求在球場區域
的中點為原點建立如圖所示的直角坐標系,求在球場區域![]() 內射門到球門
內射門到球門![]() 的最佳射門點的軌跡.
的最佳射門點的軌跡.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com