
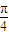 )=
)=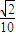 ,x∈(
,x∈( ,
,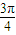 ).
). )的值.
)的值. 的范圍,進而利用同角三角函數的基本關系求得sin(x-
的范圍,進而利用同角三角函數的基本關系求得sin(x-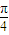 )的值,進而根據sinx=sin[(x-
)的值,進而根據sinx=sin[(x-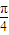 )+
)+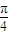 ]利用兩角和公式求得答案
]利用兩角和公式求得答案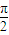 ,
,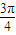 ),
),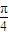 ∈(
∈(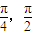 ),
),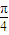 )=
)= =
=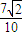 .
.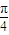 )+
)+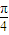 ]
]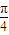 )cos
)cos +cos(x-
+cos(x- )sin
)sin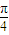
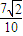 ×
×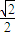 +
+ ×
×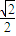 =
= .
.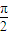 ,
,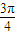 ),
),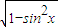 =-
=-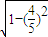 =-
=-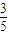 .
.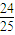 ,
,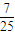 .
. )=sin2xcos
)=sin2xcos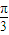 +cos2xsin
+cos2xsin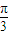
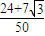 .
.

 黃岡天天練口算題卡系列答案
黃岡天天練口算題卡系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com