
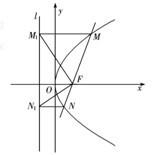
 如圖,過拋物線y2=2px(p>0)的焦點F的直線與拋物線相交于M、N兩點,自M、N向準線l作垂線,垂足分別為M1、N1
如圖,過拋物線y2=2px(p>0)的焦點F的直線與拋物線相交于M、N兩點,自M、N向準線l作垂線,垂足分別為M1、N1 ,|NN1|=|NF|=
,|NN1|=|NF|=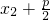 ,
, |MM1||F1M1|=
|MM1||F1M1|= ,
, |M1N2||FF1|=
|M1N2||FF1|=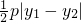 ,
, |NN1||F1N1|=
|NN1||F1N1|= ,
, •
•
 =
=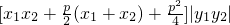 ,
,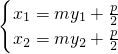 與
與 代入上式化簡可得
代入上式化簡可得 ,|NN1|=|NF|=
,|NN1|=|NF|=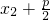 ,由此入手能夠推導(dǎo)出S22=4S1S3成立.
,由此入手能夠推導(dǎo)出S22=4S1S3成立.

 53隨堂測系列答案
53隨堂測系列答案科目:高中數(shù)學(xué) 來源: 題型:
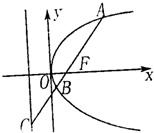 如圖,過拋物線y2=2px(p>0)的焦點F的直線l交拋物線于點A、B,交其準線于點C,若|BC|=2|BF|,且|AF|=3,則此拋物線的方程為
如圖,過拋物線y2=2px(p>0)的焦點F的直線l交拋物線于點A、B,交其準線于點C,若|BC|=2|BF|,且|AF|=3,則此拋物線的方程為查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
 如圖,過拋物線y2=2px(p>0)的焦點F的直線l交拋物線于點A、B(|AF|>|BF|),交其準線于點C,若|BC|=2|BF|,且|AF|=2,則此拋物線的方程為
如圖,過拋物線y2=2px(p>0)的焦點F的直線l交拋物線于點A、B(|AF|>|BF|),交其準線于點C,若|BC|=2|BF|,且|AF|=2,則此拋物線的方程為查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
 如圖,過拋物線y2=2px(p>0)的焦點F且傾斜角為60°的直線l交拋物線于A、B兩點,若|AF|=3,則此拋物線方程為( )
如圖,過拋物線y2=2px(p>0)的焦點F且傾斜角為60°的直線l交拋物線于A、B兩點,若|AF|=3,則此拋物線方程為( )查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com