
20、 (本小題14分)
已知函數y=x2-2ax+1(a為常數)在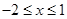 上的最小值為
上的最小值為 ,
,
試將 用a表示出來,并求出
用a表示出來,并求出 的最大值.
的最大值.
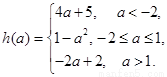
 .
.
【解析】解決二次函數的最值問題,應該先求出二次函數的對稱軸,判斷出對稱軸與區間的關系,進一步判斷出二次函數的單調性,進一步求出函數的最值.由該函數的性質可知,該函數的最小值與拋物線的對稱軸的位置有關,于是需要對對稱軸的位置進行分類討論.
解:∵y=(x-a)2+1-a2,
∴拋物線y=x2-2ax+1的對稱軸方程是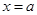 .
.
(1)當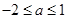 時,由圖①可知,當
時,由圖①可知,當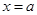 時,該函數取最小值
時,該函數取最小值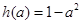 ;
;
(2) 當 時, 由圖②可知, 當
時, 由圖②可知, 當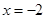 時,該函數取最小值
時,該函數取最小值 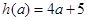 ;
;
(3) 當a>1時, 由圖③可知, 當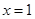 時,該函數取最小值
時,該函數取最小值
綜上,函數的最小值為
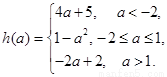 ………………8分
………………8分
 (1)當
(1)當 時,
時,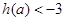
⑵當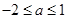 時,
時,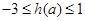
⑶當a>1時,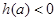 ,
,
綜上所述, .
………………14分
.
………………14分


科目:高中數學 來源: 題型:
 (本小題14分)右圖是一個直三棱柱(以
(本小題14分)右圖是一個直三棱柱(以![]() 為底面)
為底面)
被一平面所截得到的幾何體,截面為ABC.
已知![]() .
.
(1)設點O是AB的中點,證明:OC∥平面A1B1C1;
(2)證明BC⊥AC,求二面角B―AC―A1的大小;
(3)求此幾何體的體積.
查看答案和解析>>
科目:高中數學 來源:2011-2012學年廣東省肇慶市高三復習必修五綜合練習 題型:解答題
(本小題14分)如圖所示,L是海面上一條南北方向的海防警戒線,在L上點A處有一個水聲監測點,另兩個監測點B,C分別在A的正東方20 km處和54 km處.某時刻,監測點B收到發自靜止目標P的一個聲波,8s后監測點A,20 s后監測點C相繼收到這一信號.在當時氣象條件下,聲波在水中的傳播速度是1. 5 km/s.
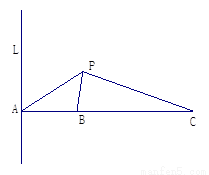
(1)設A到P的距離為 km,用
km,用 分別表示B、C到P 的距離,并求
分別表示B、C到P 的距離,并求 值;
值;
(2)求靜止目標P到海防警戒線L的距離(結果精確到0.01 km)
查看答案和解析>>
科目:高中數學 來源:2011-2012學年廣東省肇慶市高三復習必修五綜合練習 題型:解答題
(本小題14分)在等差數列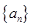 中,
中,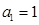 ,前
,前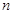 項和
項和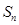 滿足條件
滿足條件 ,
,
(1)求數列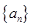 的通項公式和
的通項公式和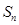 ;
;
(2)記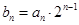 ,求數列
,求數列 的前
的前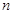 項和
項和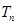
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com