
【題目】已知函數![]() .
.
(1)設![]() ,
,
①記![]() 的導函數為
的導函數為![]() ,求
,求![]() ;
;
②若方程![]() 有兩個不同實根,求實數
有兩個不同實根,求實數![]() 的取值范圍;
的取值范圍;
(2)若在![]() 上存在一點
上存在一點![]() 使
使![]() 成立,求實數
成立,求實數![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】試題分析:(1)①對![]() 進行求導,將
進行求導,將![]() 代入可得
代入可得![]() 的值,
的值,
試題解析: ![]() 的定義域
的定義域![]() ,
, ![]() 的定義域為
的定義域為![]() ,
,
(1)①![]() ,∴
,∴![]() ;②對
;②對![]() 進行二次求導,判斷
進行二次求導,判斷![]() 的單調性得其符號,從而可得
的單調性得其符號,從而可得![]() 的單調性,結合圖象的大致形狀可得
的單調性,結合圖象的大致形狀可得![]() 的取值范圍;(2)將題意轉化為
的取值范圍;(2)將題意轉化為![]() ,令
,令![]() ,題意等價于
,題意等價于![]() 在
在![]() 上的最小值小于0,對
上的最小值小于0,對![]() 進行求導,對導函數進行分類討論,判斷單調性得其最值.
進行求導,對導函數進行分類討論,判斷單調性得其最值.
②![]() ,∴
,∴![]() 遞增,又
遞增,又![]() ,所以
,所以![]() 在
在![]() 上遞減,
上遞減, ![]() 遞增。又
遞增。又![]() 趨于0的時候,
趨于0的時候, ![]() 趨于6;
趨于6; ![]() 趨于
趨于![]() 的時候,
的時候, ![]() 趨于
趨于![]() ,又
,又![]() ,所以
,所以![]() ;
;
(2)由題可得![]() ,∴
,∴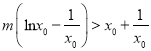 ,∴
,∴![]() ,
,
令![]() ,則
,則![]() 在
在![]() 上的最小值小于0,
上的最小值小于0,
又![]() ,
,
1,當![]() 時,即
時,即![]() ,
, ![]() 在
在![]() 上遞減,所以
上遞減,所以![]() ,解得
,解得![]() ;
;
2,當![]() 即
即![]() ,
, ![]() 在
在![]() 遞增,∴
遞增,∴![]() 解得
解得![]() ;
;
3,當![]() ,即
,即![]() ,此時要求
,此時要求![]() 又
又![]() ,
,
所以![]() ,
,
所以![]() 此時
此時![]() 不成立,
不成立,
綜上![]() 或
或![]() .
.


 能考試期末沖刺卷系列答案
能考試期末沖刺卷系列答案科目:高中數學 來源: 題型:
【題目】已知函數![]() ,(
,( ![]() ,
, ![]() ).
).
(1)若![]() ,
, ![]() ,求函數
,求函數![]() 的單調增區間;
的單調增區間;
(2)若![]() 時,不等式
時,不等式![]() 在
在![]() 上恒成立,求實數
上恒成立,求實數![]() 的取值范圍;
的取值范圍;
(3)當![]() ,
, ![]() 時,記函數
時,記函數![]() 的導函數
的導函數![]() 的兩個零點是
的兩個零點是![]() 和
和![]() (
(![]() ),求證:
),求證: ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】近年來我國電子商務行業迎來蓬勃發展的新機遇,2016年雙11期間,某平臺的銷售業績高達918億人民幣,與此同時,相關管理部門也推出了針對電商的商品和服務評價體系,現從評價系統中隨機選出200次成功的交易,并對其評價結果進行統計,對商品的好評率為![]() ,對服務的好評率為
,對服務的好評率為![]() ,其中對商品和服務都做出好評的交易為80次.
,其中對商品和服務都做出好評的交易為80次.
在犯錯誤概率不超過( )的前提下,認為商品好評與服務好評有關.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數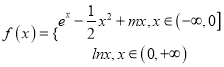 ,
, ![]() (
(![]() 為自然對數的底數).
為自然對數的底數).
(1)若函數![]() 的圖象在
的圖象在![]() 處的切線方程為
處的切線方程為![]() ,求
,求![]() ,
, ![]() 的值;
的值;
(2)若![]() 時,函數
時,函數![]() 在
在![]() 內是增函數,求
內是增函數,求![]() 的取值范圍;
的取值范圍;
(3)當![]() 時,設函數
時,設函數![]() 的圖象
的圖象![]() 與函數
與函數![]() 的圖象
的圖象![]() 交于點
交于點![]() 、
、![]() ,過線段
,過線段![]() 的中點
的中點![]() 作
作![]() 軸的垂線分別交
軸的垂線分別交![]() 、
、![]() 于點
于點![]() 、
、![]() ,問是否存在點
,問是否存在點![]() ,使
,使![]() 在
在![]() 處的切線與
處的切線與![]() 在
在![]() 處的切線平行?若存在,求出
處的切線平行?若存在,求出![]() 的橫坐標;若不存在,請說明理由.
的橫坐標;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】學校藝術節對同一類的![]() ,
,![]() ,
,![]() ,
,![]() 四項參賽作品,只評一項一等獎,在評獎揭曉前,甲、乙、丙、丁四位同學對這四項參賽作品預測如下:
四項參賽作品,只評一項一等獎,在評獎揭曉前,甲、乙、丙、丁四位同學對這四項參賽作品預測如下:
甲說:“是![]() 或
或![]() 作品獲得一等獎”;
作品獲得一等獎”;
乙說:“![]() 作品獲得一等獎”;
作品獲得一等獎”;
丙說:“![]() ,
,![]() 兩項作品未獲得一等獎”;
兩項作品未獲得一等獎”;
丁說:“是![]() 作品獲得一等獎”.
作品獲得一等獎”.
若這四位同學中只有兩位說的話是對的,則獲得一等獎的作品是__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為![]() 為參數),以該直角坐標系的原點
為參數),以該直角坐標系的原點![]() 為極點,
為極點, ![]() 軸的正半軸為極軸的極坐標系下,曲線
軸的正半軸為極軸的極坐標系下,曲線![]() 的方程為
的方程為![]() .
.
(1)求曲線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)設曲線![]() 和曲線
和曲線![]() 的交點為
的交點為![]() 、
、![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠的甲、乙兩個車間的![]() 名工人進行了勞動技能大比拼,規定:技能成績大于或等于
名工人進行了勞動技能大比拼,規定:技能成績大于或等于![]() 分為優秀,
分為優秀, ![]() 分以下為非優秀,統計成成績后,得到如下的
分以下為非優秀,統計成成績后,得到如下的![]() 列聯表,且已知在甲、乙兩個車間工人中隨機抽取
列聯表,且已知在甲、乙兩個車間工人中隨機抽取![]() 人為優秀的概率為
人為優秀的概率為![]() .
.
優秀 | 非優秀 | 合計 | |
甲車間 |
| ||
乙車間 |
| ||
合計 |
|
(1)請完成上面的列聯表;
(2)根據列聯表的數據,若按![]() 的可靠性要求,能否認為“成績與車間有關系”?
的可靠性要求,能否認為“成績與車間有關系”?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com