
【題目】已知函數![]() .
.
(1)若![]() ,求
,求![]() 的單調區間;
的單調區間;
(2)若![]() ,
,![]() ,求證:
,求證:![]() .
.
【答案】(1) ![]() 的單調遞增區間為
的單調遞增區間為![]() ,不存在遞減區間.(2)見證明
,不存在遞減區間.(2)見證明
【解析】
(1)求出![]() ,
,![]() 研究函數
研究函數![]() 的正負情況即可明確
的正負情況即可明確![]() 的正負情況,即可得到
的正負情況,即可得到![]() 的單調區間;
的單調區間;
(2) 設![]() ,證明
,證明![]() ,要證明
,要證明![]()
只需證明![]() .
.
解法一:(1)![]() 的定義域為
的定義域為![]() ,
,![]() 時,
時,![]()
![]() ,
,
所以![]()
當![]() 時,
時,![]() ,所以
,所以![]() 在
在![]() 單調遞減;
單調遞減;
當![]() 時,
時,![]() ,所以
,所以![]() 在
在![]() 單調遞增;
單調遞增;
所以![]() ,所以
,所以![]() 在
在![]() 單調遞增,
單調遞增,
即![]() 的單調遞增區間為
的單調遞增區間為![]() ,不存在遞減區間.
,不存在遞減區間.
(2)設![]() ,則
,則![]()
當![]() 時,
時,![]() ,所以
,所以![]() 在
在![]() 單調遞增;
單調遞增;
當![]() 時,
時,![]() ,所以
,所以![]() 在
在![]() 單調遞減;
單調遞減;
所以![]()
所以![]() 時,
時,![]()
即![]() ,要證明
,要證明![]()
只需證明![]()
由(1)知,![]() 在
在![]() 單調遞增,
單調遞增,
所以,當![]() 時,
時,![]() ,即
,即![]()
所以當![]() 時,
時,![]()
所以只需證明![]() ,即證明
,即證明![]()
設![]() ,則
,則![]()
所以![]() 在
在![]() 單調遞增,所以
單調遞增,所以![]() ,所以原不等式成立.
,所以原不等式成立.
綜上,當![]() ,
,![]() 時,
時,![]()
解法二:(1)同解法一
(2)同解法一得只需證明![]()
設![]() ,則
,則![]()
![]() ,
,
由![]() 得
得![]() ,即
,即![]()
因為![]() ,所以
,所以![]()
又因為![]() ,所以
,所以![]()
因為![]() ,所以
,所以![]()
所以![]() ,
,![]() 在
在![]() 單調遞增,所以
單調遞增,所以![]()
所以![]() 在
在![]() 單調遞減,所以
單調遞減,所以![]() ,即
,即![]()
綜上,當![]() ,
,![]() 時,
時,![]()
解法三:(1)同解法一
(2)同解法一得要證明![]() ,只需證明
,只需證明![]() ,
,
即證明![]() ,設
,設![]()
則![]()
由![]() ,得
,得![]() ,即
,即![]() ,所以
,所以![]() ,
,
所以![]() 在
在![]() 單調遞增,所以
單調遞增,所以![]()
即![]() ,所以
,所以![]()
綜上,當![]() ,
,![]() 時,
時,![]()
解法四:(1)同解法一
(2)同解法一得要證明![]() ,只需證明
,只需證明![]() ,
,
即證明![]() ,設
,設![]()
![]() ,設
,設![]() ,
,
因為![]() ,所以
,所以![]() ,所以
,所以![]() 在
在![]() 單調遞減,
單調遞減,
所以![]() ,
,
所以![]() 在
在![]() 單調遞增,所以
單調遞增,所以![]()
即![]() ,所以
,所以![]()
綜上,當![]() ,
,![]() 時,
時,![]()


 期末1卷素質教育評估卷系列答案
期末1卷素質教育評估卷系列答案科目:高中數學 來源: 題型:
【題目】已知點![]() 的坐標分別為
的坐標分別為![]() ,三角形
,三角形![]() 的兩條邊
的兩條邊![]() 所在直線的斜率之積是
所在直線的斜率之積是![]() .
.
(I)求點![]() 的軌跡方程;
的軌跡方程;
(II)設直線![]() 方程為
方程為![]() ,直線
,直線![]() 方程為
方程為![]() ,直線
,直線![]() 交
交![]() 于
于![]() ,點
,點![]() 關于
關于![]() 軸對稱,直線
軸對稱,直線![]() 與
與![]() 軸相交于點
軸相交于點![]() ,求
,求![]() 面積
面積![]() 關于
關于![]() 的表達式.
的表達式.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】現對某市工薪階層關于“樓市限購令”的態度進行調查,隨機抽調了50人,他們月收入的頻數分布及對“樓市限購令”贊成人數如下表.
月收入(單位百元) |
|
|
|
|
|
|
頻數 | 5 | 10 | 15 | 10 | 5 | 5 |
贊成人數 | 4 | 8 | 12 | 5 | 2 | 1 |
(1)由以上統計數據填下面2×2列聯表,并問是否有99%的把握認為“月收入以5500元為分界點對“樓市限購令”的態度有差異;
月收入不低于55百元的人數 | 月收入低于55百元的人數 | 合計 | |
贊成 | a=______________ | c=______________ | ______________ |
不贊成 | b=______________ | d=______________ | ______________ |
合計 | ______________ | ______________ | ______________ |
(2)試求從年收入位于![]() (單位:百元)的區間段的被調查者中隨機抽取2人,恰有1位是贊成者的概率。
(單位:百元)的區間段的被調查者中隨機抽取2人,恰有1位是贊成者的概率。
參考公式: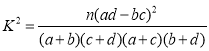 ,其中
,其中![]() .
.
參考值表:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】學生學習的自律性很重要.某學校對自律性與學生成績是否有關進行了調研,從該校學生中隨機抽取了100名學生,通過調查統計得到![]() 列聯表的部分數據如下表:
列聯表的部分數據如下表:
自律性一般 | 自律性強 | 合計 | |
成績優秀 | 40 | ||
成績一般 | 20 | ||
合計 | 50 | 100 |
(1)補全![]() 列聯表中的數據;
列聯表中的數據;
(2)判斷是否有![]() 的把握認為學生的自律性與學生成績有關.
的把握認為學生的自律性與學生成績有關.
參考公式及數據: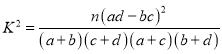 .
.
| 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在多面體![]() 中,
中,![]() 均垂直于平面
均垂直于平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
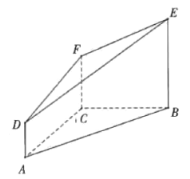
(1)過![]() 的平面
的平面![]() 與平面
與平面![]() 垂直,請在圖中作出
垂直,請在圖中作出![]() 截此多面體所得的截面,并說明理由;
截此多面體所得的截面,并說明理由;
(2)若![]() ,
,![]() ,求多面體
,求多面體![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設橢圓![]() (
(![]() )的左、右焦點為
)的左、右焦點為![]() ,右頂點為
,右頂點為![]() ,上頂點為
,上頂點為![]() .已知
.已知![]() .
.
(1)求橢圓的離心率;
(2)設![]() 為橢圓上異于其頂點的一點,以線段
為橢圓上異于其頂點的一點,以線段![]() 為直徑的圓經過點
為直徑的圓經過點![]() ,經過原點
,經過原點![]() 的直線
的直線![]() 與該圓相切,求直線
與該圓相切,求直線![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標平面上的一列點![]() 簡記為
簡記為![]() ,若由
,若由![]() 構成的數列
構成的數列![]() 滿足
滿足![]() ,(其中
,(其中![]() 是與
是與![]() 軸正方向相同的單位向量),則稱
軸正方向相同的單位向量),則稱![]() 為“
為“![]() 點列”.
點列”.
(1)試判斷:![]() ,...是否為“
,...是否為“![]() 點列”?并說明理由.
點列”?并說明理由.
(2)若![]() 為“
為“![]() 點列”,且點
點列”,且點![]() 在點
在點![]() 的右上方.任取其中連續三點
的右上方.任取其中連續三點![]() ,判斷
,判斷![]() 的形狀(銳角,直角,鈍角三角形),并證明.
的形狀(銳角,直角,鈍角三角形),并證明.
(3)若![]() 為“
為“![]() 點列”,正整數
點列”,正整數![]() 滿足:
滿足:![]() ,且
,且![]() ,求證:
,求證:![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com