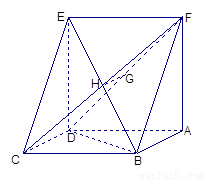
（本題滿分14分）已知如圖：平行四邊形ABCD中，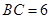
，正方形ADEF所在平面與平面ABCD垂直，G，H分別是DF，BE的中點．
（１）求證：GH∥平面CDE；
（２）若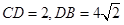
，求四棱錐F-ABCD的體積．
（1）證法１：∵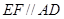
,
∴
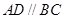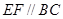且
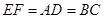
∴四邊形EFBC是平行四邊形 ∴H為FC的中點-------------2分
又∵G是FD的中點
∴
---------------------------------------4分
∵
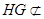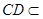平面CDE，
平面CDE
∴GH∥平面CDE -------------------------------------7分
證法２：連結EA，∵ADEF是正方形 ∴G是AE的中點 --------------1分
∴在⊿EAB中，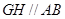
----------------------------------3分
又∵AB∥CD，∴GH∥CD，----------------------------------4分
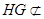∵平面CDE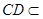，平面CDE
∴GH∥平面CDE ---------------------------------------------7分
（2）∵平面ADEF⊥平面ABCD，交線為AD
且FA⊥AD， ∴FA⊥平面ABCD.---------------------------------------------------9分
∵
, ∴
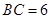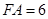又∵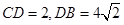
，
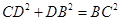
∴BD⊥CD ----------------------------------------------------------------------------------------11分
∴ 
＝
∴ 
＝
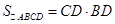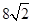
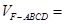
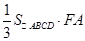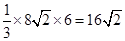-----------------------------------------14分
【解析】略
小學奪冠AB卷系列答案科目：高中數學 來源：2012-2013學年吉林省高三第一次月考文科數學試卷（解析版） 題型：解答題
（本題滿分14分）已知函數
(1)若
，求x的值；
(2)若
對于
恒成立，求實數m的取值范圍.
查看答案和解析>>
科目：高中數學 來源：2010-2011學年廣東省惠州市高三第三次調研考試數學理卷 題型：解答題
（本題滿分14分）
已知橢圓
：
的離心率為
，過坐標原點
且斜率為
的直線
與相交于
、
，
．
⑴求
、
的值；
⑵若動圓
與橢圓和直線都沒有公共點，試求
的取值范圍．
查看答案和解析>>
科目：高中數學 來源：2010-2011學年廣東省惠州市高三第三次調研考試數學理卷 題型：解答題
（（本題滿分14分）
已知梯形ABCD中，AD∥BC，∠ABC =∠BAD =
，AB=BC=2AD=4，E、F分別是AB、CD上的點，EF∥BC，AE = x，G是BC的中點．沿EF將梯形ABCD翻折，使平面AEFD⊥平面EBCF
（如圖）.
（1）當x=2時，求證：BD⊥EG ；
（2）若以F、B、C、D為頂點的三棱錐的體積記為
，
求的最大值；
（3）當取得最大值時，求二面角D-BF-C的余弦值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
，
，函數
. （Ⅰ）求
的單調增區間； （II）若在
中，角
所對的邊分別是
，且滿足：
，求
的取值范圍.
，且以下命題都為真命題：
實系數一元二次方程
的兩根都是虛數；
存在復數
同時滿足
且
.
的取值范圍.