
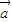 =(cosα,sinα),
=(cosα,sinα),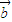 =(cosβ,sinβ),
=(cosβ,sinβ),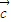 =(-1,0).
=(-1,0).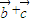 的長度的最大值;
的長度的最大值;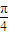 ,且
,且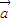 ⊥(
⊥(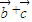 ),求cosβ的值.
),求cosβ的值. ,利用向量模的平方等于向量的平方求出
,利用向量模的平方等于向量的平方求出 的平方,利用三角函數的平方關系將其化簡,利用三角函數的有界性求出最值.
的平方,利用三角函數的平方關系將其化簡,利用三角函數的有界性求出最值.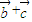 =(cosβ-1,sinβ),則
=(cosβ-1,sinβ),則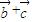 |2=(cosβ-1)2+sin2β=2(1-cosβ).
|2=(cosβ-1)2+sin2β=2(1-cosβ).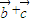 |2≤4,即0≤|
|2≤4,即0≤|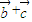 |≤2.
|≤2. 的長度的最大值為2.
的長度的最大值為2.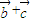 =(cosβ-1,sinβ),
=(cosβ-1,sinβ),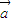 •(
•(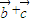 )=cosαcosβ+sinαsinβ-cosα=cos(α-β)-cosα.
)=cosαcosβ+sinαsinβ-cosα=cos(α-β)-cosα.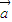 ⊥(
⊥(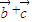 ),
),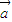 •(
•( )=0,即cos(α-β)=cosα.
)=0,即cos(α-β)=cosα.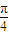 ,得cos(
,得cos(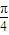 -β)=cos
-β)=cos ,
,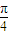 =2kπ±
=2kπ± (k∈Z),
(k∈Z),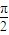 或β=2kπ,k∈Z,于是cosβ=0或cosβ=1.
或β=2kπ,k∈Z,于是cosβ=0或cosβ=1.

科目:高中數學 來源: 題型:
| a |
| b |
| c |
| π |
| 2 |
| a |
| b |
| 13 |
| 14 |
| a |
| c |
| 1 |
| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| a |
| b |
| 3 |
| a |
| b |
| 1 |
| 2 |
| π |
| 6 |
| A |
| 2 |
| 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| a |
| b |
| 3 |
| π |
| 2 |
| π |
| 2 |
| a |
| b |
| a |
| b |
查看答案和解析>>
科目:高中數學 來源: 題型:
| a |
| b |
| a |
| b |
| 2 |
| a |
| b |
| A、60° | B、90° |
| C、120° | D、150° |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com