
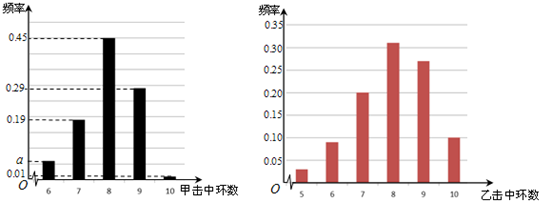
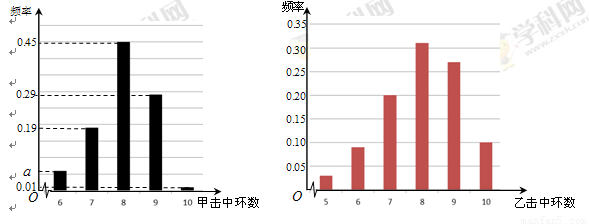
根據以往的成績記錄,甲、乙兩名隊員射擊擊中目標靶的環數的頻率分布情況如圖所示.
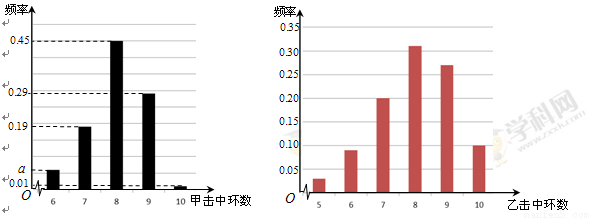
假設每名隊員每次射擊相互獨立.
(Ⅰ)求上圖中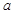 的值;
的值;
(Ⅱ)隊員甲進行三次射擊,求擊中目標靶的環數不低于8環的次數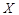 的分布列及數學期望(頻率當作概率使用);
的分布列及數學期望(頻率當作概率使用);
(Ⅲ)由上圖判斷,在甲、乙兩名隊員中,哪一名隊員的射擊成績更穩定?(結論不需證明)
(Ⅰ)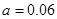 ;(Ⅱ)
;(Ⅱ)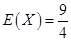 ;(Ⅲ)甲隊員的射擊成績更穩定
;(Ⅲ)甲隊員的射擊成績更穩定
【解析】
試題分析:(Ⅰ)由頻率和為1可求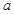 的值。(Ⅱ)從圖中可以得到擊中目標靶的環數不低于8環的概率,隊員甲進行三次射擊屬于獨立重復事件,符合二項分布。可根據獨立重復事件概率公式
的值。(Ⅱ)從圖中可以得到擊中目標靶的環數不低于8環的概率,隊員甲進行三次射擊屬于獨立重復事件,符合二項分布。可根據獨立重復事件概率公式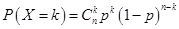 求其概率,再根據數學期望公式求其期望值,也可用二項分布列的數學期望公式求其期望值。(Ⅲ)甲隊員的射擊成績較集中、波動較小,相對穩定。
求其概率,再根據數學期望公式求其期望值,也可用二項分布列的數學期望公式求其期望值。(Ⅲ)甲隊員的射擊成績較集中、波動較小,相對穩定。
試題解析:解:(Ⅰ)由上圖可得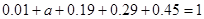 ,
,
所以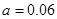 .
3分
.
3分
(Ⅱ)由圖可得隊員甲擊中目標靶的環數不低于8環的概率為
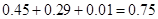 4分
4分
由題意可知隨機變量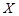 的取值為:0,1,2,3.
5分
的取值為:0,1,2,3.
5分
事件“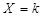 ”的含義是在3次射擊中,恰有k次擊中目標靶的環數不低于8環.
”的含義是在3次射擊中,恰有k次擊中目標靶的環數不低于8環.
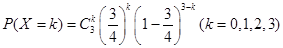
 8分
8分
即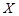 的分布列為
的分布列為
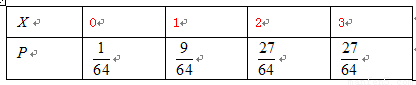
所以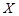 的期望是
的期望是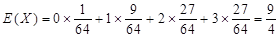 .
10分
.
10分
(Ⅲ)甲隊員的射擊成績更穩定. 13分
考點:二項分布列、數學期望及方差的意義,考查數據處理能力、運算能力。


科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
 根據以往的成績記錄,甲、乙兩名隊員射擊擊中目標靶的環數的頻率分布情況如圖所示:
根據以往的成績記錄,甲、乙兩名隊員射擊擊中目標靶的環數的頻率分布情況如圖所示:查看答案和解析>>
科目:高中數學 來源:2013-2014學年北京市海淀區高三上學期期末考試文科數學試卷(解析版) 題型:解答題
根據以往的成績記錄,甲、乙兩名隊員射擊擊中目標靶的環數的頻率分布情況如圖所示
(Ⅰ)求上圖中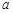 的值;
的值;
(Ⅱ)甲隊員進行一次射擊,求命中環數大于7環的概率(頻率當作概率使用);
(Ⅲ)由上圖判斷甲、乙兩名隊員中,哪一名隊員的射擊成績更穩定(結論不需證明).
查看答案和解析>>
科目:高中數學 來源:2013屆度寧夏高二下學期期中考試理科數學試卷(解析版) 題型:解答題
12分)
要從兩名同學中挑出一名,代表班級參加射擊比賽,根據以往的成績記錄同學甲擊中目標的環數為X1的分布列為
|
X1 |
5 |
6 |
7 |
8 |
9 |
10 |
|
P |
0.03 |
0.09 |
0.20 |
0.31 |
0.27 |
0.10 |
同學乙擊目標的環數X2的分布列為
|
X2 |
5 |
6 |
7 |
8 |
9 |
|
P |
0.01 |
0.05 |
0.20 |
0.41 |
0.33 |
(1)請你評價兩位同學的射擊水平(用數據作依據);
(2)如果其它班參加選手成績都在9環左右,本班應派哪一位選手參賽,如果其它班參賽選手的成績都在7環左右呢?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com