
【題目】設{an}是公比為正整數的等比數列,{bn}是等差數列,且a1a2a3=64,b1+b2+b3=﹣42,6a1+b1=2a3+b3=0.
(1)求數列{an}和{bn}的通項公式;
(2)設pn= ![]() ,數列{pn}的前n項和為Sn .
,數列{pn}的前n項和為Sn .
①試求最小的正整數n0 , 使得當n≥n0時,都有S2n>0成立;
②是否存在正整數m,n(m<n),使得Sm=Sn成立?若存在,請求出所有滿足條件的m,n;若不存在,請說明理由.
【答案】
(1)解:設等比數列{an}的公比為q>0,等差數列{bn}的公差為d,∵a1a2a3=64,b1+b2+b3=﹣42,6a1+b1=2a3+b3=0.
∴ ![]() =64,3b2=﹣42,
=64,3b2=﹣42, ![]() +b2﹣d=2a2q+b2+d=0,
+b2﹣d=2a2q+b2+d=0,
聯立解得a2=4,b2=﹣14,q=2,d=﹣2.
∴an= ![]() =4×2n﹣2=2n,bn=b2+(n﹣2)d=﹣14﹣2(n﹣2)=﹣2n﹣10
=4×2n﹣2=2n,bn=b2+(n﹣2)d=﹣14﹣2(n﹣2)=﹣2n﹣10
(2)解:①∵pn= ![]() ,
,
數列{pn}的前2n項和S2n=(a1+a3+…+a2n﹣1)+(b2+b4+…+b2n)
= ![]() ﹣14n+
﹣14n+ ![]() =
= ![]() ﹣
﹣ ![]() ﹣2n2﹣12n.
﹣2n2﹣12n.
n=1,2,3時,S2n<0.n≥4時,都有S2n>0.∴最小的正整數n0=4,使得當n≥n0時,都有S2n>0成立.
②由S1=2,S2=﹣12,S3=﹣12+23=﹣4,S4=﹣22,S5=﹣22+25=10,
S6=﹣12,S7=﹣12+27=116.
由①可知:使得當n≥4時,都有S2n>0成立,而an=2n>0.
因此n≥8時,都有Sn>0,且Sn單調遞增.
假設存在正整數m,n(m<n),使得Sm=Sn成立,
則取m=2,n=6時,Sm=Sn=﹣12成立,
由n≥8時,都有Sn>0,且Sn單調遞增,S8=90.因此Sm=Sn不可能成立.
綜上可得:只有m=2,n=6時,使得Sm=Sn成立.
【解析】(1)利用等差數列與等比數列的通項公式即可得出.(2)①pn= ![]() ,可得數列{pn}的前2n項和S2n=(a1+a3+…+a2n﹣1)+(b2+b4+…+b2n)=
,可得數列{pn}的前2n項和S2n=(a1+a3+…+a2n﹣1)+(b2+b4+…+b2n)= ![]() ﹣
﹣ ![]() ﹣2n2﹣12n.n=1,2,3時,S2n<0.n≥4時,都有S2n>0.即可得出.②由S1=2,S2=﹣12,S3=﹣4,S4=﹣22,S5=10,S6=﹣12,S7=116.由①可知:使得當n≥4時,都有S2n>0成立,而an=2n>0.因此n≥8時,都有Sn>0,且Sn單調遞增.即可得出.
﹣2n2﹣12n.n=1,2,3時,S2n<0.n≥4時,都有S2n>0.即可得出.②由S1=2,S2=﹣12,S3=﹣4,S4=﹣22,S5=10,S6=﹣12,S7=116.由①可知:使得當n≥4時,都有S2n>0成立,而an=2n>0.因此n≥8時,都有Sn>0,且Sn單調遞增.即可得出.
【考點精析】解答此題的關鍵在于理解等比數列的前n項和公式的相關知識,掌握前![]() 項和公式:
項和公式: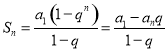 .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】已知公差為0的等差數列{an}滿足a1=1,且a1 , a3﹣2,a9成等比數列.
(1)求數列{an}的通項公式;
(2)記數列{ ![]() }的前n項和為Sn , 并求使得Sn>
}的前n項和為Sn , 并求使得Sn> ![]() +
+ ![]() 成立的最小正整數n.
成立的最小正整數n.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}的前n項和為Sn , a1=﹣ ![]() ,Sn+
,Sn+ ![]() =an﹣2(n≥2,n∈N)
=an﹣2(n≥2,n∈N)
(1)求S2 , S3 , S4的值;
(2)猜想Sn的表達式;并用數學歸納法加以證明.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C: ![]() +
+ ![]() =1(a>b>0)的離心率為
=1(a>b>0)的離心率為 ![]() ,其中左焦點F(﹣2,0).
,其中左焦點F(﹣2,0).
(1)求橢圓C的方程;
(2)若直線y=x+m與橢圓C交于不同的兩點A,B,且線段的中點M在圓x2+y2=1上,求m的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為調查高中生的數學成績與學生自主學習時間之間的相關關系,長郡中學數學教師對新入學的45名學生進行了跟蹤調查,其中每周自主做數學題的時間不少于15小時的有19人,余下的人中,在高三模擬考試中數學平均成績不足120分的占![]() ,統計成績后,得到如下的
,統計成績后,得到如下的![]() 列聯表:
列聯表:
分數大于等于120分 | 分數不足120分 | 合計 | |
周做題時間不少于15小時 | 4 | 19 | |
周做題時間不足15小時 | |||
合計 | 45 |
(1)請完成上面的![]() 列聯表,并判斷能否在犯錯誤的概率不超過0.01的前提下認為“高中生的數學成績與學生自主學習時間有關”;
列聯表,并判斷能否在犯錯誤的概率不超過0.01的前提下認為“高中生的數學成績與學生自主學習時間有關”;
(2)(ⅰ)按照分層抽樣的方法,在上述樣本中,從分數大于等于120分和分數不足120分兩組學生中抽取9名學生,設抽到的不足120分且周做題時間不足15小時的人數是![]() ,求
,求![]() 的分布列(概率用組合數算式表示);
的分布列(概率用組合數算式表示);
(ⅱ)若將頻率視為概率,從全校大于等于120分的學生中隨機抽取20人,求這些人中周做題時間不少于15小時的人數的期望和方差.
|
|
|
|
|
|
|
|
附: 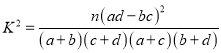
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ax3+cx(a≠0,a∈R,c∈R),當x=1時,f(x)取得極值﹣2.
(1)求函數f(x)的解析式;
(2)求函數f(x)的單調區間和極大值;
(3)若對任意x1、x2∈[﹣1,1],不等式|f(x1)﹣f(x2)|≤t恒成立,求實數t的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
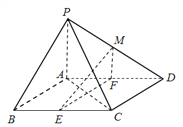
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 是平行四邊形,
是平行四邊形, ![]() ,側面
,側面![]() 底面
底面![]() ,
, ![]() ,
, ![]() ,
, ![]() 分別為
分別為![]() 的中點,點
的中點,點![]() 在線段
在線段![]() 上.
上.
(Ⅰ)求證: ![]() 平面
平面![]() ;
;
(Ⅱ)如果直線![]() 與平面
與平面![]() 所成的角和直線
所成的角和直線![]() 與平面
與平面![]() 所成的角相等,求
所成的角相等,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對一批產品的長度(單位:毫米)進行抽樣檢測,樣本容量為400,右圖為檢測結果的頻率分布直方圖,根據產品標準,單件產品長度在區間[25,30)的為一等品,在區間[20,25)和[30,35)的為二等品,其余均為三等品,則樣本中三等品的件數為 . 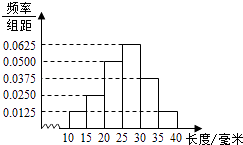
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com