
【題目】設函數f(x)=x2﹣alnx﹣(a﹣2)x.
(Ⅰ)求函數f(x)的單調區間;
(Ⅱ)若函數f(x)有兩個零點x1 , x2(1)求滿足條件的最小正整數a的值;
(Ⅲ)求證: ![]() .
.
【答案】解:(Ⅰ)f′(x)=2x﹣(a﹣2)﹣ ![]() =
= ![]() ,(x>0). 當a≤0時,f′(x)>0在(0,+∞)上恒成立,
,(x>0). 當a≤0時,f′(x)>0在(0,+∞)上恒成立,
所以函數f(x)單調遞增區間為(0,+∞),此時f(x)無單調減區間;
當a>0時,由f′(x)>0,得 ![]() ,f′(x)<0,得
,f′(x)<0,得 ![]() ,
,
所以函數f(x)的單調增區間為( ![]() ,+∞),單調減區間為(0,
,+∞),單調減區間為(0, ![]() );
);
(Ⅱ)①由(Ⅰ)可知函數f(x)有兩個零點,所以a>0,
f(x)的最小值f( ![]() )<0,即﹣a2+4a﹣4aln
)<0,即﹣a2+4a﹣4aln ![]() <0,
<0,
∵a>0,∴ ![]() ,
,
令 ![]() ,顯然h(a)在(0,+∞)上為增函數,
,顯然h(a)在(0,+∞)上為增函數,
且 ![]()
∴存在a0∈(2,3),h(a0)=0,
當a>a0時,h(a)>0;當0<a<a0時,h(a)<0,
所以滿足條件的最小正整數a=3.
又當a=3時,f(3)=3(2﹣ln3)>0, ![]() =
= ![]() <0,f(1)=0,
<0,f(1)=0,
所以a=3時,f(x)有兩個零點.
綜上所述,滿足條件的最小正整數a的值為3.
(Ⅲ)證明:不妨設0<x1<x2 ,
于是 ![]() ﹣alnx1=
﹣alnx1= ![]() ﹣alnx2 ,
﹣alnx2 ,
∴a= ![]() .,
.,
因為 ![]() =0,當x∈
=0,當x∈ ![]() 時,f′(x)<0;當x∈
時,f′(x)<0;當x∈ ![]() 時,f′(x)>0.
時,f′(x)>0.
故只要證 ![]() 即可,即證明x1+x2>
即可,即證明x1+x2> ![]() .,
.,
即證 ![]() +(x1+x2)(lnx1﹣lnx2)>
+(x1+x2)(lnx1﹣lnx2)> ![]() ﹣
﹣ ![]() ﹣2x2 .
﹣2x2 .
也就是證 ![]() <
< ![]() .
.
設 ![]() =t∈(0,1).
=t∈(0,1).
令m(t)=lnt﹣ ![]() ,則m′(t)=
,則m′(t)= ![]() ﹣
﹣ ![]() =
= ![]() .
.
∵t>0,所以m'(t)≥0,
當且僅當t=1時,m'(t)=0,所以m(t)在(0,+∞)上是增函數.
又m(1)=0,所以當m∈(0,1),m(t)<0總成立,所以原題得證
【解析】(Ⅰ)f′(x)=2x﹣(a﹣2)﹣ ![]() =
= ![]() ,(x>0).對a分類討論:a≤0,a>0,即可得出單調性.(Ⅱ)(1)由(Ⅰ)可知函數f(x)有兩個零點,所以a>0,f(x)的最小值f(
,(x>0).對a分類討論:a≤0,a>0,即可得出單調性.(Ⅱ)(1)由(Ⅰ)可知函數f(x)有兩個零點,所以a>0,f(x)的最小值f( ![]() )<0,即﹣a2+4a﹣4aln
)<0,即﹣a2+4a﹣4aln ![]() <0,可得
<0,可得 ![]() ,令
,令 ![]() ,顯然h(a)在(0,+∞)上為增函數,且
,顯然h(a)在(0,+∞)上為增函數,且 ![]() ,因此存在a0∈(2,3),h(a0)=0,進而得出小正整數a的值.(Ⅲ)不妨設0<x1<x2 , 于是
,因此存在a0∈(2,3),h(a0)=0,進而得出小正整數a的值.(Ⅲ)不妨設0<x1<x2 , 于是 ![]() ﹣alnx1=
﹣alnx1= ![]() ﹣alnx2 , 可得a=
﹣alnx2 , 可得a= ![]() .由于
.由于 ![]() =0,當x∈
=0,當x∈ ![]() 時,f′(x)>0.只要證
時,f′(x)>0.只要證 ![]() 即可,即證明x1+x2>
即可,即證明x1+x2> ![]() ,即證
,即證 ![]() <
< ![]() .設
.設 ![]() =t∈(0,1).令m(t)=lnt﹣
=t∈(0,1).令m(t)=lnt﹣ ![]() ,利用導數研究其單調性即可證明結論.
,利用導數研究其單調性即可證明結論.
【考點精析】本題主要考查了利用導數研究函數的單調性的相關知識點,需要掌握一般的,函數的單調性與其導數的正負有如下關系: 在某個區間![]() 內,(1)如果
內,(1)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞增;(2)如果
在這個區間單調遞增;(2)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞減才能正確解答此題.
在這個區間單調遞減才能正確解答此題.


科目:高中數學 來源: 題型:
【題目】為了比較注射![]() 兩種藥物后產生的皮膚皰疹的面積,選200只家兔做試驗,將這200只家兔隨機地分成兩組,毎組100只,其中一組注射藥物
兩種藥物后產生的皮膚皰疹的面積,選200只家兔做試驗,將這200只家兔隨機地分成兩組,毎組100只,其中一組注射藥物![]() ,另一組注射藥物
,另一組注射藥物![]() .
.
(1)甲、乙是200只家兔中的2只,求甲、乙分在不同組的概率;
(2)下表1和表2分別是注射藥物![]() 和
和![]() 后的試驗結果.(皰疹面積單位:
后的試驗結果.(皰疹面積單位: ![]() )
)
表1:注射藥物![]() 后皮膚皰疹面積的頻數分布表
后皮膚皰疹面積的頻數分布表

表2:注射藥物![]() 后皮膚皰疹面積的頻數分布表
后皮膚皰疹面積的頻數分布表

(ⅰ)完成下面頻率分布直方圖,并比較注射兩種藥物后皰疹面積的中位數大小;
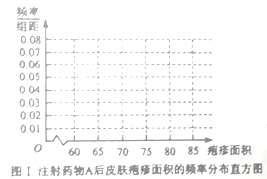
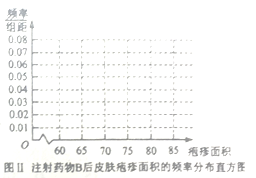
(ⅱ)完成下面![]() 列聯表,并回答能否有
列聯表,并回答能否有![]() 的把握認為“注射藥物
的把握認為“注射藥物![]() 后的皰疹面積與注射藥物
后的皰疹面積與注射藥物![]() 后的皰疹面積有差異”.
后的皰疹面積有差異”.
表3:

附: 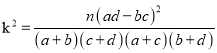
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,![]() 是邊長為
是邊長為![]() 的正方形,
的正方形,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() 與平面
與平面![]() 所成角為
所成角為![]() .
.
(Ⅰ)求證:![]() 平面
平面![]() .
.
(Ⅱ)求二面角![]() 的余弦值.
的余弦值.
(Ⅲ)設點![]() 是線段
是線段![]() 上一個動點,試確定點
上一個動點,試確定點![]() 的位置,使得
的位置,使得![]() 平面
平面![]() ,并證明你的結論.
,并證明你的結論.
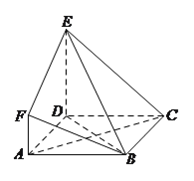
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
: ![]() 的離心率為
的離心率為![]() ,且過點
,且過點![]() ,
, ![]() ,
, ![]() 是橢圓
是橢圓![]() 上異于長軸端點的兩點.
上異于長軸端點的兩點.
(1)求橢圓![]() 的方程;
的方程;
(2)已知直線![]() :
: ![]() ,且
,且![]() ,垂足為
,垂足為![]() ,
, ![]() ,垂足為
,垂足為![]() ,若
,若![]() ,且
,且![]() 的面積是
的面積是![]() 面積的5倍,求
面積的5倍,求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】交強險是車主必須為機動車購買的險種.若普通6座以下私家車投保交強險第一年的費用(基準保費)統一為a元,在下一年續保時,實行的是費率浮動機制,保費與上一年度車輛發生道路交通事故的情況相聯系,發生交通事故的次數越多,費率也就越高,具體浮動情況如表:
交強險浮動因素和浮動費率比率表 | ||
浮動因素 | 浮動比率 | |
A1 | 上一個年度未發生有責任道路交通事故 | 下浮10% |
A2 | 上兩個年度未發生有責任道路交通事故 | 下浮20% |
A3 | 上三個及以上年度未發生有責任道路交通事故 | 下浮30% |
A4 | 上一個年度發生一次有責任不涉及死亡的道路交通事故 | 0% |
A5 | 上一個年度發生兩次及兩次以上有責任道路交通事故 | 上浮10% |
A6 | 上一個年度發生有責任道路交通死亡事故 | 上浮30% |
某機構為了研究某一品牌普通6座以下私家車的投保情況,隨機抽取了60輛車齡已滿三年的該品牌同型號私家車的下一年續保時的情況,統計得到了下面的表格:
類型 | A1 | A2 | A3 | A4 | A5 | A6 |
數量 | 10 | 5 | 5 | 20 | 15 | 5 |
以這60輛該品牌車的投保類型的頻率代替一輛車投保類型的概率,完成下列問題:
(Ⅰ)按照我國《機動車交通事故責任強制保險條例》汽車交強險價格的規定a=950.記X為某同學家的一輛該品牌車在第四年續保時的費用,求X的分布列與數學期望值;(數學期望值保留到個位數字)
(Ⅱ)某二手車銷售商專門銷售這一品牌的二手車,且將下一年的交強險保費高于基本保費的車輛記為事故車.假設購進一輛事故車虧損5000元,一輛非事故車盈利10000元:
①若該銷售商購進三輛(車齡已滿三年)該品牌二手車,求這三輛車中至多有一輛事故車的概率;
②若該銷售商一次購進100輛(車齡已滿三年)該品牌二手車,求他獲得利潤的期望值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓E: ![]() +
+ ![]() =1(a>b>0)經過點(﹣1,
=1(a>b>0)經過點(﹣1, ![]() ),其離心率e=
),其離心率e= ![]() .
.
(Ⅰ)求橢圓E的方程;
(Ⅱ)設動直線l:y=kx+m與橢圓C相切,切點為T,且l與直線x=﹣4相交于點S.
試問:在x軸上是否存在一定點,使得以ST為直徑的圓恒過該定點?若存在,求出該點的坐標;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com