
【題目】下列說法正確的是( )
A.“![]() ”是“點
”是“點![]() 到直線
到直線![]() 的距離為3”的充要條件
的距離為3”的充要條件
B.直線![]() 的傾斜角的取值范圍為
的傾斜角的取值范圍為![]()
C.直線![]() 與直線
與直線![]() 平行,且與圓
平行,且與圓![]() 相切
相切
D.離心率為![]() 的雙曲線的漸近線方程為
的雙曲線的漸近線方程為![]()
【答案】BC
【解析】
根據點到直線的距離公式判斷選項A錯誤;根據直線斜率的定義及正切函數的值域問題判斷選項B正確;根據兩直線平行的判定及直線與圓相切的判定,可判斷選項C正確;根據雙曲線漸近線的定義可判斷選項D錯誤.
選項A:由點![]() 到直線
到直線![]() 的距離為3,
的距離為3,
可得:![]() ,解得
,解得![]() 或
或![]() ,
,
“![]() ”是“點
”是“點![]() 到直線
到直線![]() 的距離為3”的充分不必要條件,
的距離為3”的充分不必要條件,
故選項A錯誤;
選項B:直線![]() 的斜率
的斜率![]() ,
,
設直線的傾斜角為![]() ,則
,則![]() 或
或![]() ,
,
![]() ,故選項B正確;
,故選項B正確;
選項C:直線![]() 可化為
可化為![]() ,
,
其與直線![]() 平行,
平行,
圓![]() 的圓心
的圓心![]() 到直線
到直線![]() 的距離為:
的距離為:
![]() ,
,
則直線![]() 與圓
與圓![]() 相切,故選項C正確;
相切,故選項C正確;
選項D:離心率為![]() ,則
,則![]()
若焦點在x軸,則雙曲線的漸近線方程為![]() ,
,
若焦點在y軸,則雙曲線的漸近線方程為![]() ,
,
故選項D錯誤.
故選:BC.


 暑假作業海燕出版社系列答案
暑假作業海燕出版社系列答案 本土教輔贏在暑假高效假期總復習云南科技出版社系列答案
本土教輔贏在暑假高效假期總復習云南科技出版社系列答案 暑假作業北京藝術與科學電子出版社系列答案
暑假作業北京藝術與科學電子出版社系列答案 第三學期贏在暑假系列答案
第三學期贏在暑假系列答案科目:高中數學 來源: 題型:
【題目】已知拋物線![]() 的焦點為
的焦點為![]() ,準線
,準線![]() 與
與![]() 軸交于點
軸交于點![]() ,點
,點![]() 在拋物線上,直線
在拋物線上,直線![]() 與拋物線
與拋物線![]() 交于另一點
交于另一點![]() .
.

(1)設直線![]() ,
,![]() 的斜率分別為
的斜率分別為![]() ,
,![]() ,求證:
,求證:![]() 常數;
常數;
(2)①設![]() 的內切圓圓心為
的內切圓圓心為![]() 的半徑為
的半徑為![]() ,試用
,試用![]() 表示點
表示點![]() 的橫坐標
的橫坐標![]() ;
;
②當![]() 的內切圓的面積為
的內切圓的面積為![]() 時,求直線
時,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】![]() 市某機構為了調查該市市民對我國申辦
市某機構為了調查該市市民對我國申辦![]() 年足球世界杯的態度,隨機選取了
年足球世界杯的態度,隨機選取了![]() 位市民進行調查,調查結果統計如下:
位市民進行調查,調查結果統計如下:
支持 | 不支持 | 合計 | |
男性市民 |
| ||
女性市民 |
| ||
合計 |
|
|
(1)根據已知數據,把表格數據填寫完整;
(2)利用(1)完成的表格數據回答下列問題:
(i)能否在犯錯誤的概率不超過![]() 的前提下認為支持申辦足球世界杯與性別有關;
的前提下認為支持申辦足球世界杯與性別有關;
(ii)已知在被調查的支持申辦足球世界杯的男性市民中有![]() 位退休老人,其中
位退休老人,其中![]() 位是教師,現從這
位是教師,現從這![]() 位退休老人中隨機抽取
位退休老人中隨機抽取![]() 人,求至多有
人,求至多有![]() 位老師的概率.
位老師的概率.
附:![]() ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市一所醫院在某時間段為發燒超過38![]() 的病人特設發熱門診,該門診記錄了連續5天晝夜溫差
的病人特設發熱門診,該門診記錄了連續5天晝夜溫差![]() (
(![]() )與就診人數
)與就診人數![]() 的資料:
的資料:
日期 | 第1天 | 第2天 | 第3天 | 第4天 | 第5天 |
晝夜溫差 | 8 | 10 | 13 | 12 | 7 |
就診人數 | 18 | 25 | 28 | 27 | 17 |
(1)求![]()
![]() 的相關系數
的相關系數![]() ,并說明晝夜溫差(
,并說明晝夜溫差(![]() )與就診人數
)與就診人數![]() 具有很強的線性相關關系.
具有很強的線性相關關系.
(2)求就診人數![]() (人)關于出晝夜溫差
(人)關于出晝夜溫差![]() (
(![]() )的線性回歸方程,預測晝夜溫差為9
)的線性回歸方程,預測晝夜溫差為9![]() 時的就診人數.
時的就診人數.
附:樣本![]()
![]() 的相關系數為
的相關系數為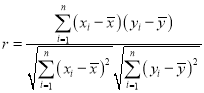 ,當
,當![]() 時認為兩個變量有很強的線性相關關系.
時認為兩個變量有很強的線性相關關系.
回歸直線方程為![]() ,其中
,其中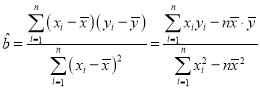 ,
,![]() .
.
參考數據:![]() ,
,![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,直線的參數方程為
中,直線的參數方程為 (
(![]() 為參數).以原點為極點,軸正半軸為極軸建立極坐標系,曲線極坐標方程為
為參數).以原點為極點,軸正半軸為極軸建立極坐標系,曲線極坐標方程為![]() ,直線與曲線交于、兩點.
,直線與曲線交于、兩點.
(1)求直線的普通方程以及曲線的直角坐標方程;
(2)若直線上有定點![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
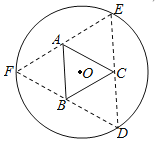
【題目】如圖,圓形紙片的圓心為![]() ,半徑為
,半徑為![]() ,該紙片上的等邊三角形
,該紙片上的等邊三角形![]() 的中心為
的中心為![]() .
.![]() ,
,![]() ,
,![]() 為圓
為圓![]() 上的點,
上的點,![]() 分別是以
分別是以![]() 為底邊的等腰三角形.沿虛線剪開后,分別以
為底邊的等腰三角形.沿虛線剪開后,分別以![]() 為折痕折起
為折痕折起![]() ,使得
,使得![]() ,
,![]() ,
,![]() 重合,得到三棱錐.當所得三棱錐體積(單位:
重合,得到三棱錐.當所得三棱錐體積(單位:![]() )最大時,
)最大時,![]() 的邊長為_________(
的邊長為_________(![]() ).
).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com