Question

如圖，在△ABC中，∠BAC=60°，線段AD⊥平面ABC，AH⊥平面DBC，H為垂足.

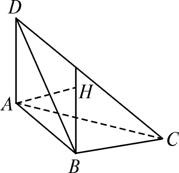
求證：H不可能是△BCD的垂心.

Answer 1

解析：證明“不可能”無法下手，從反面“可能”考慮，用反證法證明.

證明：假設H是△BCD的垂心，則BH⊥CD.

∵AH⊥平面DBC，DC平面DBC，∴AH⊥DC.

∵AH∩BH＝H,∴CD⊥平面ABH.

又AB平面ABH,∴CD⊥AB.

∵AD⊥平面ABC，AB平面ABC,∴AD⊥AB.

由于AD∩CD＝D,∴AB⊥平面ACD.

∵AC平面ACD,∴AB⊥AC.這與已知中∠BAC＝60°相矛盾.

∴假設不成立.故H不可能是△BCD的垂心.

點評：(1)“不可能”類型的問題用反證法證明.“不可能”的反面是“可能”.

(2)注意反證法的證題過程.實際上∠BAC只要不是90°，這個題型的方法總是一樣的.