
【題目】在棱長為![]() 的正方體
的正方體![]() 中,O是AC的中點,E是線段D1O上一點,且D1E=λEO.
中,O是AC的中點,E是線段D1O上一點,且D1E=λEO.
(1)若λ=1,求異面直線DE與CD1所成角的余弦值;
(2)若平面CDE⊥平面CD1O,求λ的值.

【答案】(1)![]() (2)λ=2
(2)λ=2
【解析】分析:以![]() 為單位正交基底建立如圖所示的空間直角坐標系
為單位正交基底建立如圖所示的空間直角坐標系![]() ,寫出各點的坐標,
,寫出各點的坐標,
(1)求出異面直線![]() 與
與![]() 1的方向向量用數量積公式兩線夾角的余弦值(或補角的余弦值)
1的方向向量用數量積公式兩線夾角的余弦值(或補角的余弦值)
(2)求出兩個平面的法向量,由于兩個平面垂直,故它們的法向量的內積為0,由此方程求參數![]() 的值即可.
的值即可.
詳解:
(1)以![]() 為單位正交基底建立如圖所示的空間直角坐標系
為單位正交基底建立如圖所示的空間直角坐標系![]() .
.
則A(1,0,0),![]() ,
,![]() ,D1(0,0,1),
,D1(0,0,1),
E![]() ,
,
于是![]() ,
,![]() .
.
由cos![]() =
=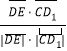 =
=![]() .
.
所以異面直線AE與CD1所成角的余弦值為![]() .
.
(2)設平面CD1O的向量為m=(x1,y1,z1),由m·![]() =0,m·
=0,m·![]() =0
=0
得 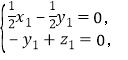 取x1=1,得y1=z1=1,即m=(1,1,1) . ………8分
取x1=1,得y1=z1=1,即m=(1,1,1) . ………8分
由D1E=λEO,則E![]() ,
,![]() =
=![]() .10分
.10分
又設平面CDE的法向量為n=(x2,y2,z2),由n·![]() =0,n·
=0,n·![]() =0.
=0.
得 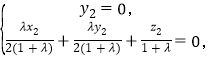 取x2=2,得z2=-λ,即n=(-2,0,λ) .12分
取x2=2,得z2=-λ,即n=(-2,0,λ) .12分
因為平面CDE⊥平面CD1F,所以m·n=0,得![]() .
.


 云南師大附小一線名師提優作業系列答案
云南師大附小一線名師提優作業系列答案 沖刺100分單元優化練考卷系列答案
沖刺100分單元優化練考卷系列答案科目:高中數學 來源: 題型:
【題目】(本題滿分12分)袋中裝有黑色球和白色球共7個,從中任取2個球都是白色球的概率為![]() .現有甲、乙兩人從袋中輪流摸出1個球,甲先摸,乙后摸,然后甲再摸,……,摸后均不放回,直到有一人摸到白色球后終止.每個球在每一次被摸出的機會都是等可能的,用X表示摸球終止時所需摸球的次數.
.現有甲、乙兩人從袋中輪流摸出1個球,甲先摸,乙后摸,然后甲再摸,……,摸后均不放回,直到有一人摸到白色球后終止.每個球在每一次被摸出的機會都是等可能的,用X表示摸球終止時所需摸球的次數.
(1)求隨機變量X的分布列和均值E(X);
(2)求甲摸到白色球的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某超市隨機選取![]() 位顧客,記錄了他們購買甲、乙、丙、丁四種商品的情況,整理成如下統計表,其中“√”表示購買,“×”表示未購買.
位顧客,記錄了他們購買甲、乙、丙、丁四種商品的情況,整理成如下統計表,其中“√”表示購買,“×”表示未購買.
| 甲 | 乙 | 丙 | 丁 |
| √ | × | √ | √ |
| × | √ | × | √ |
| √ | √ | √ | × |
| √ | × | √ | × |
85 | √ | × | × | × |
| × | √ | × | × |
(Ⅰ)估計顧客同時購買乙和丙的概率;
(Ⅱ)估計顧客在甲、乙、丙、丁中同時購買![]() 中商品的概率;
中商品的概率;
(Ⅲ)如果顧客購買了甲,則該顧客同時購買乙、丙、丁中那種商品的可能性最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了鞏固全國文明城市創建成果,今年吉安市開展了拆除違章搭建鐵皮棚專項整治行為.為了了解市民對此項工作的“支持”與“反對”態度,隨機從存在違章搭建的戶主中抽取了男性、女性共![]() 名進行調查,調查結果如下:
名進行調查,調查結果如下:
支持 | 反對 | 合計 | |
男性 |
|
|
|
女性 |
|
|
|
合計 |
|
|
|
(1)根據以上數據,判斷是否有![]() 的把握認為對此項工作的“支持”與“反對”態度與“性別”有關;
的把握認為對此項工作的“支持”與“反對”態度與“性別”有關;
(2)現從參與調查的女戶主中按此項工作的“支持”與“反對”態度用分層抽樣的方法抽取![]() 人,從抽取的
人,從抽取的![]() 人中再隨機地抽取
人中再隨機地抽取![]() 人贈送小禮品,記這
人贈送小禮品,記這![]() 人中持“支持”態度的有
人中持“支持”態度的有![]() 人,求
人,求![]() 的分布列與數學期望.
的分布列與數學期望.
參考公式:![]() ,其中
,其中![]() .
.
參考數據:
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 圖像上有一最低點
圖像上有一最低點![]() ,若圖像上各點縱坐標不變,橫坐標縮為原來的
,若圖像上各點縱坐標不變,橫坐標縮為原來的![]() 倍,再向左平移
倍,再向左平移![]() 個單位得
個單位得![]() ,又
,又![]() 的所有根從小到大依次相差
的所有根從小到大依次相差![]() 個單位,則
個單位,則![]() 的解析式為__________.
的解析式為__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() :
:![]() (
(![]() )的焦點為
)的焦點為![]() ,拋物線上存在一點
,拋物線上存在一點![]() 到焦點的距離為3,且點
到焦點的距離為3,且點![]() 在圓
在圓![]() :
:![]() 上.
上.
(Ⅰ)求拋物線![]() 的方程;
的方程;
(Ⅱ)已知橢圓![]() :
:![]() (
(![]() )的一個焦點與拋物線
)的一個焦點與拋物線![]() 的焦點重合,且離心率為
的焦點重合,且離心率為![]() .直線
.直線![]() :
:![]() 交橢圓
交橢圓![]() 于
于![]() ,
,![]() 兩個不同的點,若原點
兩個不同的點,若原點![]() 在以線段
在以線段![]() 為直徑的圓的外部,求實數
為直徑的圓的外部,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com