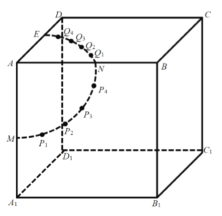
【題目】如圖，棱長為2的正方體
中，點
分別為棱
的中點，以
為圓心，1為半徑，分別在面
和面
內(nèi)作弧
和
，并將兩弧各五等分，分點依次為
、
、
、
、
、
以及
、
、
、
、
、
．一只螞蟻欲從點
出發(fā)，沿正方體的表面爬行至
，則其爬行的最短距離為________．參考數(shù)據(jù)：
；
；
）
【答案】
【解析】
根據(jù)空間位置關(guān)系，將平面旋轉(zhuǎn)后使得各點在同一平面內(nèi)，結(jié)合角的關(guān)系即可求得兩點間距離的三角函數(shù)表達(dá)式.根據(jù)所給參考數(shù)據(jù)即可得解.
棱長為2的正方體
中，點
分別為棱
的中點，以
為圓心，1為半徑，分別在面
和面
內(nèi)作弧
和
.
將平面
繞
旋轉(zhuǎn)至與平面
共面的位置，如下圖所示：
則
，所以
；
將平面繞
旋轉(zhuǎn)至與平面
共面的位置，將繞
旋轉(zhuǎn)至與平面共面的位置，如下圖所示：
則
，所以
；
因為
，且由誘導(dǎo)公式可得
，
所以最短距離為
，
故答案為：.
學(xué)期復(fù)習(xí)一本通學(xué)習(xí)總動員期末加暑假延邊人民出版社系列答案科目：高中數(shù)學(xué) 來源： 題型：
【題目】某個微信群某次進(jìn)行的搶紅包活動中，群主所發(fā)紅包的總金額為10元，被隨機分配為2.49元、1.32元、2.19元、0.63元、3.37元共5份，供甲、乙等5人搶，每人只能搶一次，則甲、乙二人搶到的金額之和不低于4元的概率是（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù)
的圖象的一條對稱軸為
，則下列結(jié)論中正確的是（ ）
A.
是最小正周期為
的奇函數(shù)
B.
是圖像的一個對稱中心
C.在
上單調(diào)遞增
D.先將函數(shù)
圖象上各點的縱坐標(biāo)縮短為原來的
，然后把所得函數(shù)圖象再向左平移
個單位長度，即可得到函數(shù)的圖象.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù)
，
為其導(dǎo)函數(shù)．
（Ⅰ）當(dāng)
，
時，求函數(shù)
的極值；
（Ⅱ）設(shè)
，當(dāng)
時，對任意的
，都有
恒成立，求
的取值范圍．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知函數(shù)
，其中
（1）若函數(shù)
在區(qū)間
上不單調(diào)，求
的取值范圍；
（2）若函數(shù)在區(qū)間上有極大值
，求的值.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知橢圓
的離心率為
是
上一點．
（1）求橢圓
的方程；
（2）設(shè)
是
分別關(guān)于兩坐標(biāo)軸及坐標(biāo)原點的對稱點，平行于
的直線
交
于異于
的兩點
．點
關(guān)于原點的對稱點為
．證明：直線
與
軸圍成的三角形是等腰三角形．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知數(shù)列
中，
，且
．
（Ⅰ）求數(shù)列的通項公式；
（Ⅱ）設(shè)數(shù)列的前
項和為
，求滿足
的所有正整數(shù)的值．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】如圖，已知
內(nèi)接于圓O，AB是圓O的直徑，四邊形DBCE為平行四邊形，F是CD的中點，
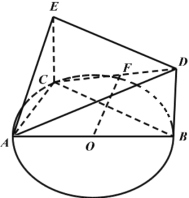
（1）證明：
平面ADE；
（2）若四邊形DBCE為矩形，且四邊形DBCE所在的平面與圓O所在的平面互相垂直，
，AE與圓O所在的平面的線面角為60°.求二面角
的平面角的余弦值.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
