
【題目】某險種的基本保費為![]() (單位:元),繼續購買該險種的投保人稱為續保人,續保人本年度的保費與其上年度出險次數的關聯如下:
(單位:元),繼續購買該險種的投保人稱為續保人,續保人本年度的保費與其上年度出險次數的關聯如下:
上年度出險次數 | 0 | 1 | 2 | 3 | 4 |
|
保費 |
|
|
|
|
|
|
設該險種一續保人一年內出險次數與相應概率如下:
一年內出險次數 | 0 | 1 | 2 | 3 | 4 |
|
概率 | 0.30 | 0.15 | 0.20 | 0.20 | 0.10 | 0.05 |
(1)求一續保人本年度的保費高于基本保費的概率;
(2)已知一續保人本年度的保費高于基本保費,求其保費比基本保費高出![]() 的概率.
的概率.
 中考解讀考點精練系列答案
中考解讀考點精練系列答案科目:高中數學 來源: 題型:
【題目】為了鞏固全國文明城市創建成果,今年吉安市開展了拆除違章搭建鐵皮棚專項整治行為.為了了解市民對此項工作的“支持”與“反對”態度,隨機從存在違章搭建的戶主中抽取了男性、女性共![]() 名進行調查,調查結果如下:
名進行調查,調查結果如下:
支持 | 反對 | 合計 | |
男性 |
|
|
|
女性 |
|
|
|
合計 |
|
|
|
(1)根據以上數據,判斷是否有![]() 的把握認為對此項工作的“支持”與“反對”態度與“性別”有關;
的把握認為對此項工作的“支持”與“反對”態度與“性別”有關;
(2)現從參與調查的女戶主中按分層抽樣的方法抽取![]() 人進行調查,分別求出所抽取的
人進行調查,分別求出所抽取的![]() 人中持“支持”和“反對”態度的人數;
人中持“支持”和“反對”態度的人數;
(3)現從(2)中所抽取的![]() 人中,再隨機抽取
人中,再隨機抽取![]() 人贈送小品,求恰好抽到
人贈送小品,求恰好抽到![]() 人持“支持”態度的概率?
人持“支持”態度的概率?
參考公式:![]() ,其中
,其中![]() .
.
參考數據:
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某屆奧運會上,中國隊以26金18銀26銅的成績稱金牌榜第三、獎牌榜第二,某校體育愛好者在高三 年級一班至六班進行了“本屆奧運會中國隊表現”的滿意度調查(結果只有“滿意”和“不滿意”兩種),從被調查的學生中隨機抽取了50人,具體的調查結果如表:
班號 | 一班 | 二班 | 三班 | 四班 | 五班 | 六班 |
頻數 | 5 | 9 | 11 | 9 | 7 | 9 |
滿意人數 | 4 | 7 | 8 | 5 | 6 | 6 |
(1)在高三年級全體學生中隨機抽取一名學生,由以上統計數據估計該生持滿意態度的概率;
(2)若從一班至二班的調查對象中隨機選取4人進行追蹤調查,記選中的4人中對“本屆奧運會中國隊表現”不滿意的人數為ξ,求隨機變量ξ的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知f(x)是定義域為(0,+∞)的單調函數,若對任意的x∈(0,+∞),都有 ![]() ,且方程|f(x)﹣3|=x3﹣6x2+9x﹣4+a在區間(0,3]上有兩解,則實數a的取值范圍是( )
,且方程|f(x)﹣3|=x3﹣6x2+9x﹣4+a在區間(0,3]上有兩解,則實數a的取值范圍是( )
A.0<a≤5
B.a<5
C.0<a<5
D.a≥5
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知曲線C1:y=cos x,C2:y=sin (2x+![]() ),則下面結論正確的是( )
),則下面結論正確的是( )
A. 把C1上各點的橫坐標伸長到原來的2倍,縱坐標不變,再把得到的曲線向右平移![]() 個單位長度,得到曲線C2
個單位長度,得到曲線C2
B. 把C1上各點的橫坐標伸長到原來的2倍,縱坐標不變,再把得到的曲線向左平移![]() 個單位長度,得到曲線C2
個單位長度,得到曲線C2
C. 把C1上各點的橫坐標縮短到原來的![]() 倍,縱坐標不變,再把得到的曲線向右平移
倍,縱坐標不變,再把得到的曲線向右平移![]() 個單位長度,得到曲線C2
個單位長度,得到曲線C2
D. 把C1上各點的橫坐標縮短到原來的![]() 倍,縱坐標不變,再把得到的曲線向左平移
倍,縱坐標不變,再把得到的曲線向左平移![]() 個單位長度,得到曲線C2
個單位長度,得到曲線C2
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,以坐標原點為極點,
中,以坐標原點為極點,![]() 軸的正半軸為極軸建立極坐標系.已知點
軸的正半軸為極軸建立極坐標系.已知點![]() 的直角坐標為
的直角坐標為![]() ,曲線
,曲線![]() 的極坐標方程為
的極坐標方程為![]() ,直線
,直線![]() 過點
過點![]() 且與曲線
且與曲線![]() 相交于
相交于![]() ,
,![]() 兩點.
兩點.
(1)求曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)若![]() ,求直線
,求直線![]() 的直角坐標方程.
的直角坐標方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=|4x﹣a|+|4x+3|,g(x)=|x﹣1|﹣|2x|.
(1)解不等式g(x)>﹣3;
(2)若存在x1∈R,也存在x2∈R,使得f(x1)=g(x2)成立,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,已知橢圓 ![]() (a>b>0)的離心率為
(a>b>0)的離心率為 ![]() ,焦點到相應準線的距離為1.
,焦點到相應準線的距離為1. 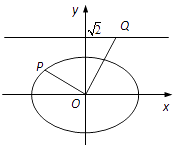
(1)求橢圓的標準方程;
(2)若P為橢圓上的一點,過點O作OP的垂線交直線 ![]() 于點Q,求
于點Q,求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在直三棱柱![]() (側棱垂直于底面)中,
(側棱垂直于底面)中,![]() ,
,![]() ,
,![]() ,
,![]() .
.

(1)證明:![]() 平面
平面![]() ;
;
(2)若![]() 是
是![]() 的中點,在線段
的中點,在線段![]() 上是否存在一點
上是否存在一點![]() 使
使![]() 平面
平面![]() ?若存在,請確定點
?若存在,請確定點![]() 的位置;若不存在,也請說明理由.
的位置;若不存在,也請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com