分析:(I)由
an存在,且A=an(A>0),對an+1=a+兩邊取極限得A=a+,解得A=.又A>0,∴A=.(II)
由an=bn+A,an+1=a+得bn+1+A=a+.由此可知
bn+1=-.
(III)
令|b1|≤,得|a-(a+)|≤.所以
|(-a)|≤.由此可求出a的取值范圍.
解答:解:(I)由
an存在,且A=an(A>0),對an+1=a+兩邊取極限得A=a+,解得A=.又A>0,∴A=.(II)
由an=bn+A,an+1=a+得bn+1+A=a+.∴
bn+1=a-A+=-+=-.即bn+1=-對n=1,2,都成立(III)
令|b1|≤,得|a-(a+)|≤.∴
|(-a)|≤.∴
-a≤1,解得a≥.現證明當a≥時,|bn|≤對n=1,2,都成立.(i)當n=1時結論成立(已驗證).
(ii)假設當
n=k(k≥1)時結論成立,即|bk|≤,那么|bk+1|=≤×故只須證明
≤,即證A|bk+A|≥2對a≥成立.由于A==,
而當a≥時,-a≤1,∴A≥2.∴
|bk+A|≥A-|bk|≥2-≥1,即A|bk+A|≥2.故當a≥時,|bk+1|≤×=.即n=k+1時結論成立.
根據(i)和(ii)可知結論對一切正整數都成立.
故
|bn|≤對n=1,2,都成立的a的取值范圍為[,+∞). 點評:本小題主要考查數列、數列極限的概念和數學歸納法,考查靈活運用數學知識分析問題和解決問題的能力.



 ,n=1,2,…。
,n=1,2,…。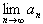 (將A用a表示);
(將A用a表示);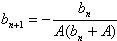 ;
;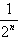 對n=1,2,…都成立,求a的取值范圍。
對n=1,2,…都成立,求a的取值范圍。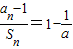 .數列{bn}中,bn=an•lgan.
.數列{bn}中,bn=an•lgan.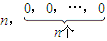 ;
;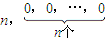 .設Sm=am+am+1+…+an,m=1,2,…,n,求證
.設Sm=am+am+1+…+an,m=1,2,…,n,求證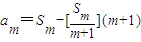 ,其中
,其中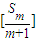 表示不超過
表示不超過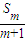 的最大整數.
的最大整數.