
【題目】若函數(shù)![]() (
(![]() ,
,![]() 是自然對數(shù)的底數(shù),
是自然對數(shù)的底數(shù),![]() )存在唯一的零點,則實數(shù)
)存在唯一的零點,則實數(shù)![]() 的取值范圍為______.
的取值范圍為______.
【答案】![]()
【解析】
函數(shù)![]() 存在唯一的零點等價于函數(shù)
存在唯一的零點等價于函數(shù)![]() 與函數(shù)
與函數(shù)![]() 的圖像只有一個交點.∵
的圖像只有一個交點.∵![]() ,
,![]() ,∴函數(shù)
,∴函數(shù)![]() 與函數(shù)
與函數(shù)![]() 的圖像的唯一交點為
的圖像的唯一交點為![]() .對
.對![]() 求導,可得
求導,可得![]() 的單調性及斜率范圍,又
的單調性及斜率范圍,又![]() 是最小正周期為2.最大值為
是最小正周期為2.最大值為![]() 的正弦型函數(shù),畫出草圖,比較
的正弦型函數(shù),畫出草圖,比較![]() 與
與![]() 在x=1處斜率即可.
在x=1處斜率即可.
函數(shù)![]() (
(![]() ,
,![]() 是自然對數(shù)的底數(shù),
是自然對數(shù)的底數(shù),![]() )存在唯一的零點等價于函數(shù)
)存在唯一的零點等價于函數(shù)![]() 與函數(shù)
與函數(shù)![]() 的圖像只有一個交點.
的圖像只有一個交點.
∵![]() ,
,![]() ,
,
∴函數(shù)![]() 與函數(shù)
與函數(shù)![]() 的圖像的唯一交點為
的圖像的唯一交點為![]() .
.
又∵![]() ,且
,且![]() ,
,![]() ,
,
∴![]() 在
在![]() 上恒小于零,即
上恒小于零,即![]() 在
在![]() 上為單調遞減函數(shù).
上為單調遞減函數(shù).
又∵![]() ,當且僅當
,當且僅當![]() ,即
,即![]() 時等號成立,且
時等號成立,且![]() 是最小正周期為2.最大值為
是最小正周期為2.最大值為![]() 的正弦型函數(shù),
的正弦型函數(shù),
∴可得函數(shù)![]() 與函數(shù)
與函數(shù)![]() 的大致圖像如圖所示.
的大致圖像如圖所示.
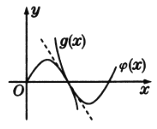
∴要使函數(shù)![]() 與函數(shù)
與函數(shù)![]() 的圖像只有唯一一個交點,則
的圖像只有唯一一個交點,則![]() .
.
∵![]() ,
,![]() ,
,
∴![]() ,解得
,解得![]() .
.
對∵![]() ,∴實數(shù)
,∴實數(shù)![]() 的取值范圍為
的取值范圍為![]() .
.
故答案為:![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數(shù)學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,橢圓![]() 的右焦點、右頂點分別為F,A,過原點的直線與橢圓C交于點P、Q(點P在第一象限內),連結PA,QF.若
的右焦點、右頂點分別為F,A,過原點的直線與橢圓C交于點P、Q(點P在第一象限內),連結PA,QF.若![]() ,
,![]() 的面積是
的面積是![]() 面積的3倍.
面積的3倍.
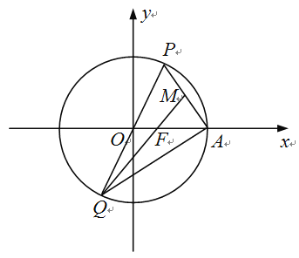
(1)求橢圓C的標準方程;
(2)已知M為線段PA的中點,連結QA,QM.
①求證:Q,F,M三點共線;
②記直線QP,QM,QA的斜率分別為![]() ,
,![]() ,
,![]() ,若
,若![]() ,求
,求![]() 的面積.
的面積.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,在直角梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,點
,點![]() 是線段
是線段![]() 的中點,將
的中點,將![]() ,
,![]() 分別沿
分別沿![]() ,
,![]()
向上折起,使![]() ,
,![]() 重合于點
重合于點![]() ,得到三棱錐
,得到三棱錐![]() .試在三棱錐
.試在三棱錐![]() 中,
中,
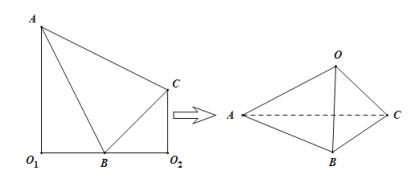
(1)證明:平面![]() 平面
平面![]() ;
;
(2)求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知數(shù)列![]() 是首項為1的等差數(shù)列,數(shù)列
是首項為1的等差數(shù)列,數(shù)列![]() 是公比不為1的等比數(shù)列,且滿足
是公比不為1的等比數(shù)列,且滿足![]() ,
,![]() ,
,![]()
(1)求數(shù)列![]() ,
,![]() 的通項公式;
的通項公式;
(2)令![]() ,記數(shù)列
,記數(shù)列![]() 的前n項和為
的前n項和為![]() ,求證:對任意的
,求證:對任意的![]() ,都有
,都有![]() ;
;
(3)若數(shù)列![]() 滿足
滿足![]() ,
,![]() ,記
,記![]() ,是否存在整數(shù)
,是否存在整數(shù)![]() ,使得對任意的
,使得對任意的![]() 都有
都有![]() 成立?若存在,求出
成立?若存在,求出![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】科研人員在對人體脂肪含量和年齡之間關系的研究中,獲得了一些年齡和脂肪含量的簡單隨機樣本數(shù)據,如下表:
| 26 | 27 | 39 | 41 | 49 | 53 | 56 | 58 | 60 | 61 |
| 14.5 | 17.8 | 21.2 | 25.9 | 26.3 | 29.6 | 31.4 | 33.5 | 35.2 | 34.6 |
根據上表的數(shù)據得到如下的散點圖.
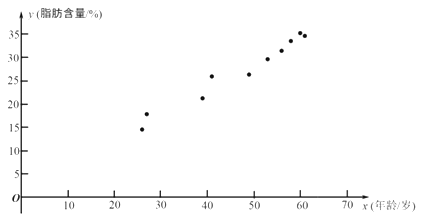
(1)根據上表中的樣本數(shù)據及其散點圖:
(i)求![]() ;
;
(i)計算樣本相關系數(shù)(精確到0.01),并刻畫它們的相關程度.
(2)若![]() 關于
關于![]() 的線性回歸方程為
的線性回歸方程為![]() ,求
,求![]() 的值(精確到0.01),并根據回歸方程估計年齡為50歲時人體的脂肪含量.
的值(精確到0.01),并根據回歸方程估計年齡為50歲時人體的脂肪含量.
附:參考數(shù)據:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
參考公式:相關系數(shù)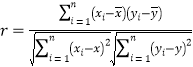
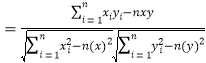
回歸方程![]() 中斜率和截距的最小二乘估計公式分別為
中斜率和截距的最小二乘估計公式分別為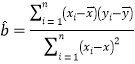 ,
,![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在直角坐標系![]() 中,傾斜角為
中,傾斜角為![]() 的直線
的直線![]() 經過坐標原點
經過坐標原點![]() ,曲線
,曲線![]() 的參數(shù)方程為
的參數(shù)方程為![]() (
(![]() 為參數(shù)).以點
為參數(shù)).以點![]() 為極點,
為極點,![]() 軸的非負半軸為極軸建立極坐標系,曲線
軸的非負半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求![]() 與
與![]() 的極坐標方程;
的極坐標方程;
(2)設![]() 與
與![]() 的交點為
的交點為![]() 、
、![]() ,
,![]() 與
與![]() 的交點為
的交點為![]() 、
、![]() ,且
,且![]() ,求
,求![]() 值.
值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】為加快新能源汽車產業(yè)發(fā)展,推進節(jié)能減排,某年國家對消費者購買新能源汽車給予補貼,其中對純電動乘用車補貼標準如下表:
新能源汽車補貼標準 | |||
車輛類型 | 續(xù)駛里程 | ||
|
|
| |
純電動乘用車 | 3.5萬元/輛 | 5萬元/輛 | 6萬元/輛 |
某校研究學習小組從汽車市場上隨機選取了![]() 輛純電動乘用車,根據其續(xù)駛里程
輛純電動乘用車,根據其續(xù)駛里程![]() (單次充電后能行駛的最大里程)作出了如下的頻率與頻數(shù)的統(tǒng)計表:
(單次充電后能行駛的最大里程)作出了如下的頻率與頻數(shù)的統(tǒng)計表:
分組 | 頻數(shù) | 頻率 |
| 2 | 0.2 |
| 5 |
|
|
|
|
合計 |
| 1 |
(1)若從這![]() 輛純電動乘用車中任選2輛,求選到的2輛車續(xù)駛里程都不低于150km的概率.
輛純電動乘用車中任選2輛,求選到的2輛車續(xù)駛里程都不低于150km的概率.
(2)若以頻率作為概率,設![]() 為購買一輛純電動乘用車獲得的補貼,求
為購買一輛純電動乘用車獲得的補貼,求![]() 的分布列和數(shù)學期望
的分布列和數(shù)學期望![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】日晷是中國古代用來測定時間的儀器,利用與晷面垂直的晷針投射到晷面的影子來測定時間.把地球看成一個球(球心記為O),地球上一點A的緯度是指OA與地球赤道所在平面所成角,點A處的水平面是指過點A且與OA垂直的平面.在點A處放置一個日晷,若晷面與赤道所在平面平行,點A處的緯度為北緯40°,則晷針與點A處的水平面所成角為( )

A.20°B.40°
C.50°D.90°
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某市環(huán)保部門對市中心每天的環(huán)境污染情況進行調查研究后,發(fā)現(xiàn)一天中環(huán)境綜合污染指數(shù)![]() 與時刻
與時刻![]() (時)的關系為
(時)的關系為![]() ,
,![]() ,其中
,其中![]() 是與氣象有關的參數(shù),且
是與氣象有關的參數(shù),且![]() .若用每天
.若用每天![]() 的最大值為當天的綜合污染指數(shù),并記作
的最大值為當天的綜合污染指數(shù),并記作![]() .
.
(1)令![]() ,
,![]() ,求
,求![]() 的取值范圍;
的取值范圍;
(2)求![]() 的表達式,并規(guī)定當
的表達式,并規(guī)定當![]() 時為綜合污染指數(shù)不超標,求當
時為綜合污染指數(shù)不超標,求當![]() 在什么范圍內時,該市市中心的綜合污染指數(shù)不超標.
在什么范圍內時,該市市中心的綜合污染指數(shù)不超標.
查看答案和解析>>
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com