
【題目】已知函數![]() .
.
(Ⅰ)當![]() 時,求曲線
時,求曲線![]() 在
在![]() 處的切線方程;
處的切線方程;
(Ⅱ)當![]() 時,若不等式
時,若不等式![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍.
的取值范圍.
【答案】(I)![]() ;(II)
;(II)![]()
【解析】
試題分析:(I)求出![]() 時,
時,![]() ,根據直線方程的點斜式可得切線方程;(II)當
,根據直線方程的點斜式可得切線方程;(II)當![]() 時,若不等式
時,若不等式![]() 恒成立等價于
恒成立等價于![]() ,通過討論
,通過討論![]() 的范圍,得到其在
的范圍,得到其在![]() 上的單調性,分別求出求出最小值,得到
上的單調性,分別求出求出最小值,得到![]() 的范圍,最后取并集即得實數
的范圍,最后取并集即得實數![]() 的取值范圍.
的取值范圍.
試題解析:(I)當![]() 時,
時,![]() ,
,
即曲線![]() 在
在![]() 處的切線的斜率為
處的切線的斜率為![]() ,又
,又![]() ,
,
所以所求切線方程為![]() .
.
(II)當![]() 時,若不等式
時,若不等式![]() 恒成立
恒成立![]()
易知![]()
若![]() ,則
,則![]() 恒成立,
恒成立,![]() 在R上單調遞增;
在R上單調遞增;
又![]() ,所以當
,所以當![]() 時,
時,![]() ,符合題意.
,符合題意.
若![]() ,由
,由![]() ,解得
,解得![]() ,則當
,則當![]() 時,
時,![]() ,
,![]() 單調遞減;
單調遞減;
當![]() 時,
時,![]() ,
,![]() 單調遞增.
單調遞增.
所以![]() 時,函數
時,函數![]() 取得最小值.
取得最小值.
則當![]() ,即
,即![]() 時,則當
時,則當![]() 時,
時,![]() ,符合題意.
,符合題意.
當![]() ,即
,即![]() 時,則當
時,則當![]() 時,
時,![]() 單調遞增,
單調遞增,![]() ,不符合題意.
,不符合題意.
綜上,實數![]() 的取值范圍是
的取值范圍是![]() (沒有綜上扣一分)
(沒有綜上扣一分)


科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,已知圓C1:(x+3)2+(y-1)2=4和圓C2:(x-4)2+(y-5)2=4.若直線l過點A(4,0),且被圓C1截得的弦長為2![]() ,求直線l的方程;
,求直線l的方程;
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2015年10月十八屆五中全會決定2016年1月1日起全國統一實施全面兩孩政策,為了了解適齡民眾對放開生育二胎政策的態度,某市進行了一次民意調查,參與調查的100位市民中,年齡分布情況如下圖所示,并得到適齡民眾對放開生育二胎政策的態度數據如下表:
生二胎 | 不生二胎 | 合計 | |
25~35歲 | 10 | ||
35~50歲 | 30 | ||
合計 | 100 |
(1)填寫上面的![]() 列聯表;
列聯表;
(2)根據調查數據,有多少的把握認為“生二胎與年齡有關”,說明理由;
(3)調查對象中決定生二胎的民眾有六人分別來自三個不同的家庭且為父子,各自家庭都有一個約定:父親先生二胎,然后兒子生二胎,則這三個家庭“二胎出生的日期的先后順序”有多少種?
參考數據:
| 0.15 | 0.10 | 0.05 | 0.010 |
| 2.072 | 2.706 | 3.841 | 6.635 |
(參考公式:![]() ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知關于![]() 的一次函數
的一次函數![]() .
.
(1)設集合![]() 和
和![]() ,分別從集合
,分別從集合![]() 和
和![]() 中隨機取一個數作為
中隨機取一個數作為![]() 和
和![]() ,求函數
,求函數![]() 是增函數的概率;
是增函數的概率;
(2)實數![]() 滿足條件
滿足條件 ,求函數
,求函數![]() 的圖象經過第一、二、三象限的概率.
的圖象經過第一、二、三象限的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2017年天貓五一活動結束后,某地區研究人員為了研究該地區在五一活動中消費超過3000元的人群的年齡狀況,隨機在當地消費超過3000元的群眾中抽取了500人作調查,所得概率分布直方圖如圖所示:記年齡在![]() ,
, ![]() ,
, ![]() 對應的小矩形的面積分別是
對應的小矩形的面積分別是![]() ,且
,且![]() .
.
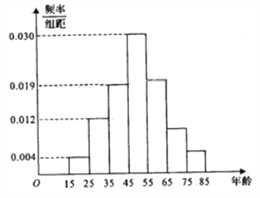
(1)以頻率作為概率,若該地區五一消費超過3000元的有30000人,試估計該地區在五一活動中消費超過3000元且年齡在![]() 的人數;
的人數;
(2)若按照分層抽樣,從年齡在![]() 的人群中共抽取6人,再從這6人中隨機抽取2人作深入調查,求至少有1人的年齡在
的人群中共抽取6人,再從這6人中隨機抽取2人作深入調查,求至少有1人的年齡在![]() 內的概率.
內的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在如圖所示的空間幾何體中,平面![]() 平面
平面![]() ,
,![]() 與
與![]() 都是邊長為2的等邊三角形,
都是邊長為2的等邊三角形,![]() ,
,![]() 與平面
與平面![]() 所成的角為
所成的角為![]() ,且點E在平面
,且點E在平面![]() 上的射影落在
上的射影落在![]() 的平分線上.
的平分線上.
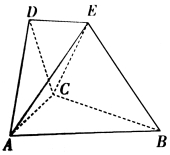
(1)求證:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】衡州市英才中學貫徹黨的教育方針,促進學生全面發展,積極組織開展了豐富多樣的社團活動,根據調查,英才中學在傳統民族文化的繼承方面開設了“泥塑”、“剪紙”、“曲藝”三個社團,三個社團參加的人數如下表所示:
社團 | 泥塑 | 剪紙 | 曲藝 |
人數 | 320 | 240 | 200 |
為調查社團開展情況,學校社團管理部采用分層抽樣的方法從中抽取一個容量為![]() 的樣本,已知從“剪紙”社團抽取的同學比從“泥塑”社團抽取的同學少2人。
的樣本,已知從“剪紙”社團抽取的同學比從“泥塑”社團抽取的同學少2人。
(1)求三個社團分別抽取了多少同學;
(2)若從“剪紙”社團抽取的同學中選出2人擔任該社團活動監督的職務,已知“剪紙”社團被抽取的同學中有2名女生,求至少有1名女同學被選為監督職務的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() ,直線
,直線![]() 經過點A (1,0).
經過點A (1,0).
(1)若直線![]() 與圓C相切,求直線
與圓C相切,求直線![]() 的方程;
的方程;
(2)若直線![]() 與圓C相交于P,Q兩點,求三角形CPQ面積的最大值,并求此時直線
與圓C相交于P,Q兩點,求三角形CPQ面積的最大值,并求此時直線![]() 的方程.
的方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com