
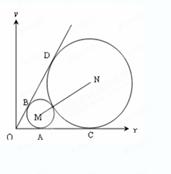
如圖,已知圓心坐標為![]() 的圓
的圓![]() 與
與![]() 軸及直線
軸及直線![]() 分別相切于
分別相切于![]() 、
、![]() 兩點,另一圓
兩點,另一圓![]() 與圓
與圓![]() 外切、且與
外切、且與![]() 軸及直線
軸及直線![]() 分別相切于
分別相切于![]() 、
、![]() 兩點.
兩點.
(1)求圓![]() 和圓
和圓![]() 的方程;
的方程;
(2)過點B作直線![]() 的平行線
的平行線![]() ,求直線
,求直線![]() 被圓
被圓![]() 截得的弦的長度.
截得的弦的長度.

解:(1)由于⊙M與∠BOA的兩邊均相切,故M到OA及OB的距離均為⊙M的半徑,則M在∠BOA的平分線上,
同理,N也在∠BOA的平分線上,即O,M,N三點共線,
且OMN為∠BOA的平分線,
∵M的坐標為![]() ,∴M到
,∴M到![]() 軸的距離為1,即⊙M的半徑為1,
軸的距離為1,即⊙M的半徑為1,
則⊙M的方程為![]() ,-
,-
設⊙N的半徑為![]() ,其與
,其與![]() 軸的的切點為C,連接MA、MC,
軸的的切點為C,連接MA、MC,
由Rt△OAM∽Rt△OCN可知,OM:ON=MA:NC,
即![]() ,
,
則OC=![]() ,則⊙N的方程為
,則⊙N的方程為![]() ;
;
(2)由對稱性可知,所求的弦長等于過A點直線MN的平行線被⊙![]() 截得的弦的長度,此弦的方程是
截得的弦的長度,此弦的方程是![]() ,即:
,即:![]() ,
,
圓心N到該直線的距離d=![]() ,則弦長=
,則弦長=![]() .
.
另解:求得B(![]() ),再得過B與MN平行的直線方程
),再得過B與MN平行的直線方程![]() ,
,
圓心N到該直線的距離![]() =
=![]() ,則弦長=
,則弦長=![]() .
.
(也可以直接求A點或B點到直線MN的距離,進而求得弦長)


科目:高中數學 來源: 題型:
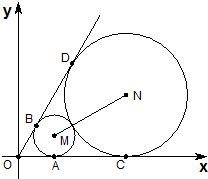 如圖,已知圓心坐標為M(
如圖,已知圓心坐標為M(| 3 |
| 3 |
| 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:
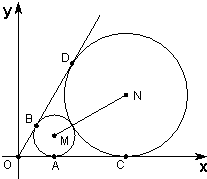 如圖,已知圓心坐標為(
如圖,已知圓心坐標為(| 3 |
| 3 |
| 3 |
查看答案和解析>>
科目:高中數學 來源:黑龍江省牡丹江一中10-11學年高一下學期期末考試數學(理) 題型:解答題
(本小題滿分12分)如圖,已知圓心坐標為 的圓
的圓 與
與 軸及直線
軸及直線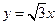 分別相切于
分別相切于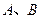 兩點,另一圓
兩點,另一圓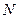 與圓
與圓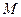 外切,且與
外切,且與 軸及直線
軸及直線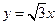 分別相切于
分別相切于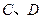 兩點.
兩點.
(1)求圓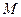 和圓
和圓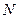 的方程;(2)過點
的方程;(2)過點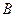 作直線
作直線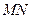 的平行線
的平行線 ,求直線
,求直線 被圓
被圓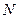 截得的弦的長度.
截得的弦的長度.
查看答案和解析>>
科目:高中數學 來源:2015屆江西南昌八一、中學、麻丘中學高二10月聯考數學卷(解析版) 題型:解答題
如圖,已知圓心坐標為 的圓
的圓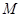 與
與 軸及直線
軸及直線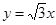 均相切,切點分別為
均相切,切點分別為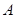 、
、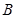 ,另一圓
,另一圓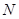 與圓
與圓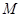 、
、 軸及直線
軸及直線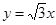 均相切,切點分別為
均相切,切點分別為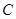 、
、 .
.
(1)求圓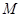 和圓
和圓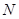 的方程;
的方程;
(2)過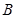 點作
點作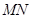 的平行線
的平行線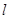 ,求直線
,求直線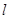 被圓
被圓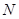 截得的弦的長度;
截得的弦的長度;
查看答案和解析>>
科目:高中數學 來源:黑龍江省10-11學年高一下學期期末考試數學(理) 題型:解答題
(本小題滿分12分)如圖,已知圓心坐標為 的圓
的圓 與
與 軸及直線
軸及直線 分別相切于
分別相切于 兩點,另一圓
兩點,另一圓 與圓
與圓 外切,且與
外切,且與 軸及直線
軸及直線 分別相切于
分別相切于 兩點.
兩點.
(1)求圓 和圓
和圓 的方程;(2)過點
的方程;(2)過點 作直線
作直線 的平行線
的平行線 ,求直線
,求直線 被圓
被圓 截得的弦的長度.
截得的弦的長度.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com