日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

精英家教網 > 高中數學 > 題目詳情

已知函數且)有兩個零點,則的取值范圍是_______.

練習冊系列答案
相關習題

科目：高中數學 來源： 題型：

（2008•湖北模擬）對于函數f（x），若存在x0∈R，使f（x0）=x0成立，則稱x0為f（x）的不動點．如果函數f(x)=
x2+a
bx-c
(b，c∈N*)有且僅有兩個不動點0、2，且f(-2)＜-
1
2
．
（1）試求函數f（x）的單調區間；
（2）已知各項不為零的數列{an}滿足4Sn•f(
1
an
)=1，求證：-
1
an+1
＜ln
n+1
n
＜-
1
an
；
（3）設bn=-
1
an
，Tn為數列{bn}的前n項和，求證：T2008-1＜ln2008＜T2007．

查看答案和解析>>

科目：高中數學 來源： 題型：

對于函數f（x），若存在x0∈R，使f（x0）=x0成立，則稱x0為f（x）的不動點．如果函數f(x)=
x2+a
bx-c
(b，c∈N*)有且僅有兩個不動點0和2，且f(-2)＜-
1
2
．
（1）求實數b，c的值；
（2）已知各項不為零的數列{an}的前n項之和為Sn，并且4Sn•f(
1
an
)=1，求數列{an}的通項公式；
（3）求證：(1-
1
an
)an+1＜
1
e
＜(1-
1
an
)an．

查看答案和解析>>

科目：高中數學 來源： 題型：

對于函數f（x），若存在xo∈R，使f（xo）=xo成立，則稱xo為f（x）的不動點．如果函數f（x）=
x2+a
bx-c
（b，c∈N*）有且僅有兩個不動點0和2，且f（-2）＜-
1
2
．
（1）試求函數f（x）的單調區間；
（2）已知各項不為零的數列{an}滿足4Sn•f（
1
an
）=1，求證：-
1
an+1
＜ln
n+1
n
＜-
1
an
；
（3）設bn=-
1
an
，Tn為數列{bn}的前n項和，求證：T2009-1＜ln2009＜T2008．

查看答案和解析>>

科目：高中數學 來源： 題型：

（08年黃岡中學一模理） (本小題滿分14分)對于函數f(x)，若存在，使成立，則稱x0為f(x)的不動點. 如果函數有且僅有兩個不動點0，2，且

（1）試求函數f(x)的單調區間；

（2）已知各項不為零且不為1的數列{an}滿足，求證：；

（3）設，為數列{bn}的前n項和，求證：

查看答案和解析>>

科目：高中數學 來源：2008-2009學年重慶七中高三（上）12月段考數學試卷（理科）（解析版） 題型：解答題

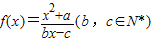對于函數f（x），若存在x∈R，使f（x）=x成立，則稱x為f（x）的不動點．如果函數有且僅有兩個不動點0、2，且．
（1）試求函數f（x）的單調區間；
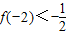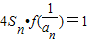（2）已知各項不為零的數列{an}滿足，求證：；
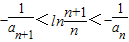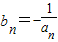（3）設，Tn為數列{bn}的前n項和，求證：T2008-1＜ln2008＜T2007．

查看答案和解析>>

同步練習冊答案
主站蜘蛛池模板： 一区二区福利 | 国产超碰人人爽人人做人人爱 | 日韩视频精品在线 | 日本成年人免费网站 | 影音先锋亚洲资源 | 日本不卡一区二区 | 九九热这里只有精品6 | 国产一区 | 亚洲成人免费网址 | 色吧久久 | 精品欧美乱码久久久久久 | 日韩在线中文字幕 | 日韩欧美视频一区二区三区 | 中国妞xxxhd露脸偷拍视频 | 成人欧美一区二区三区黑人 | 欧洲成人午夜免费大片 | 久久久精品影院 | 欧美在线国产 | 日本私人网站在线观看 | 国产免费成人在线 | 黄色片免费在线观看 | 日本免费不卡 | 午夜视频免费 | 欧美性猛交一区二区三区精品 | 国产永久免费观看 | 91久久国产综合久久 | 欧美亚洲国产精品 | 国产成人免费av一区二区午夜 | 精产国产伦理一二三区 | 天天添 | 国产福利在线免费 | 五月婷婷导航 | 一区二区三区欧美在线 | 国产精品一区二区三区在线 | 成人国产精品免费网站 | 午夜激情视频免费 | 国产精品毛片无码 | 日本亚洲欧美 | 久久99国产一区二区三区 | 91亚洲视频在线观看 | 北条麻妃国产九九九精品小说 |