已知函數f(x)=ax2+bx+c(a>0且bc≠0).
(1)若|f(0)|=|f(1)|=|f(-1)|=1,試求f(x)的解析式;
(2)令g(x)=2ax+b,若g(1)=0,又f(x)的圖象在x軸上截得的弦的長度為l,且0<|x1-x2|≤2,試確定c-b的符號.
【答案】
分析:(1)由|f(0)|=|f(1)|=|f(-1)|=1,我們可以構造關于a,b,c的方程,結合二次函數的性質,解方程即可得到函數f(x)的解析式;
(2)聯立兩個函數的解析式,結合韋達定理,我們可表示出|x
1-x
2|,結合0<|x
1-x
2|≤2,及a>0且bc≠0等條件,我們可以構造關于a,b,c的不等式,解不等式即可得到答案.
解答:解:(1)由已知|f(1)|=|f(-1)|,有|a+b+c|=|a-b+c|,(a+b+c)
2=(a-b+c)
2,可得4b(a+c)=0.
∵bc≠0,∴b≠0.∴a+c=0.
又由a>0有c<0.
∵|c|=1,于是c=-1,則a=1,|b|=1.
∴f(x)=x
2±x-1.
(2)g(x)=2ax+b,由g(1)=0有2a+b=0,b<0.
設方程f(x)=0的兩根為x
1、x
2.
∴x
1+x
2=-
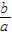
=2,x
1x
2=
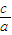
.
則|x
1-x
2|=
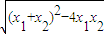
=
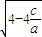
.
由已知0<|x
1-x
2|≤2,
∴0≤
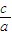
<1.
又∵a>0,bc≠0,
∴c>0.
∴c-b>0.
點評:本題考查的知識點是一元二次不等式的應用,函數解析式的求法,二次函數的性質,根據已知條件,結合二次函數的性質,將已知條件轉化為關于a,b,c的方程(或不等式)是解答本題的關鍵.

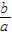 =2,x1x2=
=2,x1x2=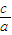 .
.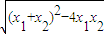 =
=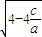 .
.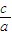 <1.
<1.

 中考利劍中考試卷匯編系列答案
中考利劍中考試卷匯編系列答案 教育世家狀元卷系列答案
教育世家狀元卷系列答案 黃岡課堂作業本系列答案
黃岡課堂作業本系列答案 單元加期末復習先鋒大考卷系列答案
單元加期末復習先鋒大考卷系列答案