電視臺應某企業之約播放兩套連續劇．其中，連續劇甲每次播放時間為80 min，廣告時間為1 min，收視觀眾為60萬；連續劇乙每次播放時間為40 min，廣告時間為1 min，收視觀眾為20萬．已知此企業與電視臺達成協議，要求電視臺每周至少播放6 min廣告，而電視臺每周播放連續劇的時間不能超過320分鐘．問兩套連續劇各播多少次，才能獲得最高的收視率？
分析：先設每周播放連續劇甲x次，播放連續劇乙y次，收視率為z．寫出約束條件與目標函數，欲求兩套連續劇各播多少次，才能獲得最高的收視率，即求可行域中的最優解，在線性規劃的解答題中建議使用直線平移法求出最優解，即將目標函數看成是一條直線，分析目標函數Z與直線截距的關系，進而求出最優解．
解答：解：將所給信息用下表表示．
設每周播放連續劇甲x次，播放連續劇乙y次，收視率為z．
則目標函數為z=60x+20y，
約束條件為
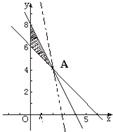
，作出可行域如圖．（5分）
作平行直線系y=-3x+
，由圖可知，當直線過點A時縱截距
最大．（6分）
解方程組
，得點A的坐標為（2，4），z
max=60x+20y=200（萬）．（11分）
所以，電視臺每周應播放連續劇甲2次，播放連續劇乙4次，才能獲得最高的收視率．
點評：在解決線性規劃的應用題時，其步驟為：①分析題目中相關量的關系，列出不等式組，即約束條件?②由約束條件畫出可行域?③分析目標函數Z與直線截距之間的關系?④使用平移直線法求出最優解?⑤還原到現實問題中．屬于基礎題．
