
【題目】已知函數![]() ,
,![]() 的最大值為
的最大值為![]() .
.
(1)求![]() 的值;
的值;
(2)試推斷方程![]() 是否有實數解?若有實數解,請求出它的解集.
是否有實數解?若有實數解,請求出它的解集.
【答案】(1)![]() ;(2)無實數解
;(2)無實數解
【解析】
(1)由題意,對函數f(x)=-x+lnx求導數,研究出函數在定義域上的單調性,判斷出最大值,即可求出;
(2)由于函數的定義域是正實數集,故方程|2x(x-lnx)|=2lnx+x可變為![]() ,再分別研究方程兩邊對應函數的值域,即可作出判斷.
,再分別研究方程兩邊對應函數的值域,即可作出判斷.
(1)已知函數![]() ,則
,則![]() ,
,
可得![]() ,
,
令![]() ,x=1,
,x=1,
當0<x<1時,f′(x)>0;當x>1時,f′(x)<0.
∴f(x)在(0,1)上是增函數,在(1,+∞)上是減函數,
∴![]() ;
;
(2)|2x(xlnx)|=2lnx+x可得![]() ,
,
由(1)知f(x)max=f(1)=1,即x+lnx≤1,
∴|xlnx|≥1,
又令![]() ,
,![]() ,
,
令g′(x)>0,得0<x<e;令g′(x)<0,得x>e,
∴g(x)的增區間為(0,e),減區間為(e,+∞),
∴![]() ,∴g(x)<1,
,∴g(x)<1,
∴|xlnx|>g(x),即![]() 恒成立,
恒成立,
∴方程![]() 即方程|2x(xlnx)|=2lnx+x沒有實數解.
即方程|2x(xlnx)|=2lnx+x沒有實數解.


 世紀百通主體課堂小學課時同步達標系列答案
世紀百通主體課堂小學課時同步達標系列答案 世紀百通優練測系列答案
世紀百通優練測系列答案科目:高中數學 來源: 題型:
【題目】“六藝”源于中國周朝的貴族教育體系,具體包括“禮、樂、射、御、書、數”.某校在周末學生業余興趣活動中開展了“六藝”知識講座,每藝安排一節,連排六節,則滿足“禮”與“樂”必須排在前兩節,“射”和“御”兩講座必須相鄰的不同安排種數為________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國南宋數學家楊輝在所著的《詳解九章算法》一書中用如圖所示的三角形解釋二項展開式的系數規律,現把楊輝三角中的數從上到下,從左到右依次排列,得數列:1,1,1,1,2,1,1,3,3,1,1,4,6,4,1,…,記作數列![]() ,若數列
,若數列![]() 的前
的前![]() 項和為
項和為![]() ,則
,則![]() _____.
_____.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C:![]() 的離心率為
的離心率為![]() ,且過點
,且過點![]() .
.
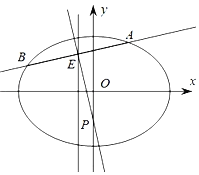
(1)求橢圓C的方程;
(2)直線l交橢圓C于不同的兩點A、B,且![]() 中點E在直線
中點E在直線![]() 上,線段
上,線段![]() 的垂直平分線交y軸于點
的垂直平分線交y軸于點![]() ,求m的取值范圍.
,求m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給出下列敘述:
①正四面體![]() 的棱長為
的棱長為![]() ,
,![]() 是棱
是棱![]() 的中點,則異面直線
的中點,則異面直線![]() 與
與![]() 所成角的余弦值是
所成角的余弦值是![]() ;
;
②在等比數列![]() 中前
中前![]() 項和為
項和為![]() ,前
,前![]() 項和為
項和為![]() ,則前
,則前![]() 項和為
項和為![]() ;
;
③直線![]() 關于直線
關于直線![]() 對稱的直線方程為
對稱的直線方程為![]() ;
;
④若![]() ,
,![]() ,且
,且![]() ,則
,則![]() 的最小值為
的最小值為![]() ;
;
其中所有正確敘述的序號是_____________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙兩人各進行![]() 次射擊,甲每次擊中目標的概率為
次射擊,甲每次擊中目標的概率為![]() ,乙每次擊中目標的概率
,乙每次擊中目標的概率![]() ,
,
(Ⅰ)記甲擊中目標的次數為![]() ,求
,求![]() 的概率分布及數學期望;
的概率分布及數學期望;
(Ⅱ)求甲恰好比乙多擊中目標![]() 次的概率.
次的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com