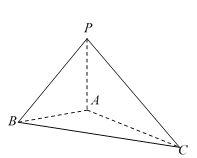
【題目】如圖所示，在三棱錐
中，
，
，
，
，
.
(Ⅰ)求證：平面
平面
；
(Ⅱ)
為棱
上一點，試確定點的位置，使得直線
與平面
所成角的正弦值為
.
【答案】(Ⅰ)見解析；(Ⅱ) 
為棱
的中點
【解析】
（Ⅰ）由余弦定理得AC＝
，由勾股定理得PA⊥AC，由PA⊥BC，得PA⊥平面ABC，由此能證明平面ABC⊥平面PAC．
（Ⅱ）設BC的中點為D，連結AD，以AB，AD，AP所在直線分別為x軸，y軸，z軸，建立空間直角坐標系，利用向量能求出E為棱AC的中點．
(Ⅰ)在
中，由余弦定理得
，即
，
又
，
，
，
，
又
，
，
平面
，
平面，
平面
，
平面
平面.
(Ⅱ)設
的中點為
，連接
，
，
，又
，
.
如圖所示，以
所在直線分別為
軸，
軸，
軸，建立空間直角坐標系
.
則
，
，
，
，
，
，
，
設
(
)，則
設平面
的法向量為
，則
，令
，可得
，
，設直線
與平面所成角為
，
則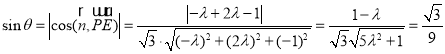
，
整理得
，
，
，
為棱的中點.
一線名師權威作業本系列答案科目：高中數學 來源： 題型：
【題目】某校進入高中數學競賽復賽的學生中，高一年級有8人，高二年級有16人，高三年級有32人，現釆用分層抽樣的方法從這些學生中抽取7人進行釆訪.
（1）求應從各年級分別抽取的人數；
（2）若從抽取的7人中再隨機抽取2人做進一步了解（注高一學生記為
，高二學生記為
，高三學生記為
，
①列出所有可能的抽取結果；
②求抽取的2人均為高三年級學生的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】一個口袋內裝有大小相同的5個球，其中3個白球，2個黑球，從中一次摸出兩個球．
（1）共有多少個基本事件？
（2）摸出的兩個都是白球的概率是多少？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】（1）已知雙曲線的中心在原點，焦點在x軸上，實軸長為4，漸近線方程為
．求雙曲線的標準方程；
（2）過（1）中雙曲線上一點P的直線分別交兩條漸近于
兩點，且P是線段AB的中點，求證：
為常數；
（3）我們知道函數
的圖象是由雙曲線
的圖象逆時針旋轉45°得到的，函數
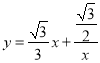的圖象也是雙曲線，請嘗試寫出曲線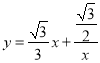的性質（不必證明）．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系xOy中，曲線C的參數方程是
（
為參數），把曲線C的橫坐標縮短為原來的
，縱坐標縮短為原來的一半，得到曲線
直線l的普通方程是
，以坐標原點O為極點，x軸正半軸為極軸建立極坐標系.
（1）求直線l的極坐標方程和曲線的普通方程；
（2）記射線
（
）與交于點A，與l交于點B，求
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
