已知函數
的圖象關于原點成中心對稱, 試判斷
在區間
上的單調性,并證明你的結論.
解: 答f(x)在[-4,4]上是單調遞減函數.
證明:∵函數f(x)的圖象關于原點成中心對稱,
則f(x)是奇函數,。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。2分
所以a=1,b=0,。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。4分
于是f(x)=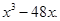
。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。6分
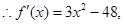。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。8分
∴當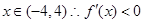
。。。。。。。。。。。。。。。。。。。。。。。。。。。。。10分
所以f(x)在[-4,4]上是單調遞減函數.。。。。。。。。。。。。。。。。。。。。。。。12分
【解析】略
科目：高中數學 來源： 題型：022
(
山東勝利一中模擬)已知下列命題：A.
；
B.函數f(|x|－1)的圖象向左平移1個單位后得到的函數圖象解析式為y=f(|x|)；
C.函數y=f(1＋x)的圖象與函數y=f(1－x)的圖象關于y軸對稱；
D.滿足條件
，∠B=60°，AB=1的△ABC有兩個．其中正確命題的代號是_________．（按照原順序將所有正確命題的代號都寫出來）
查看答案和解析>>
科目：高中數學 來源： 題型：022
(2006
北京東城模擬)已知函數
，給出下列命題：
A.f(x)不可能為偶函數；
B.當f(0)=f(2)時，f(x)的圖象必關于直線x=1對稱；
C.若
，則f(x)在區間[a，＋∞)上是增函數；
D.f(x)
有最小值
，其中正確命題的代號是________(按照原順序將你認為正確的命題的代號都填上)．查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com