
【題目】選修4-4:坐標系與參數方程
在直角坐標系中,以坐標原點![]() 為極點,
為極點, ![]() 軸的非負半軸為極軸建立極坐標系.已知點
軸的非負半軸為極軸建立極坐標系.已知點![]() 的極坐標為
的極坐標為![]() ,圓
,圓![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),(1)直線
為參數),(1)直線![]() 過
過![]() 且與圓
且與圓![]() 相切,求直線
相切,求直線![]() 的極坐標方程;(2)過點
的極坐標方程;(2)過點![]() 且斜率為
且斜率為![]() 的直線
的直線![]() 與圓
與圓![]() 交于
交于![]() ,
, ![]() 兩點,若
兩點,若![]() ,求實數
,求實數![]() 的值.
的值.
【答案】(1)![]() 或
或![]() .(2)-3.
.(2)-3.
【解析】試題分析:(1)先根據直線與圓相切求直線![]() 的直角坐標方程(注意斜率不存在的情形),再利用
的直角坐標方程(注意斜率不存在的情形),再利用![]() 將直角坐標方程化為極坐標方程(2)設直線
將直角坐標方程化為極坐標方程(2)設直線![]() 的參數方程,根據參數幾何意義得
的參數方程,根據參數幾何意義得![]() ,將直線
,將直線![]() 的參數方程代入圓
的參數方程代入圓![]() 的方程,并利用韋達定理得
的方程,并利用韋達定理得![]() ,解方程可得實數
,解方程可得實數![]() 的值.注意滿足判別式大于零.
的值.注意滿足判別式大于零.
試題解析:解:(1)![]() 的直角坐標為
的直角坐標為![]() ,圓
,圓![]() 的直角坐標方程為
的直角坐標方程為![]() ,
,
設直線![]() ,即
,即![]() ,
,
因為直線![]() 與圓
與圓![]() 相切,所以
相切,所以![]() ,解得
,解得![]() ,
,
此時直線![]() 的方程為
的方程為![]() ,
,
若直線![]() 的斜率不存在時,直線
的斜率不存在時,直線![]() 的方程為
的方程為![]() ,
,
所以直線![]() 的極坐標方程為
的極坐標方程為![]() 或
或![]() .
.
(2)將直線![]() 的參數方程
的參數方程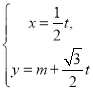 (
(![]() 時參數)代入圓
時參數)代入圓![]() 的方程
的方程![]() ,
,
得: ![]() ,
, ![]()
![]() ,
,
設![]() ,
, ![]() ,則
,則![]() ,因為
,因為![]() ,所以
,所以![]() ,
,
所以![]() ,解得
,解得![]() ,
,
由![]() 知,所求
知,所求![]() 的值為-3.
的值為-3.


 寒假樂園北京教育出版社系列答案
寒假樂園北京教育出版社系列答案科目:高中數學 來源: 題型:
【題目】已知圓F1:(x+1)2+y2=16,定點F2(1,0),A是圓F1上的一動點,線段F2A的垂直平分線交半徑F1A于P點.
(1)求P點的軌跡C的方程;
(2)四邊形EFGH的四個頂點都在曲線C上,且對角線EG,FH過原點O,
若kEGkFH=-![]() ,求證:四邊形EFGH的面積為定值,并求出此定值.
,求證:四邊形EFGH的面積為定值,并求出此定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校課改實行選修走班制,現有甲,乙,丙,丁四位學生準備選修物理,化學,生物三個科目.每位學生只選修一個科目,且選修其中任何一個科目是等可能的.
(1)恰有2人選修物理的概率;
(2)選修科目個數ξ的分布列及期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】近代統計學的發展起源于二十世紀初,它是在概率論的基礎上發展起來的,統計性質的工作可以追溯到遠古的“結繩記事”和《二十四史》中大量的關于我人口、錢糧、 水文、天文、地震等資料的記錄.近幾年,霧霾來襲,對某市該年11月份的天氣情況進行統計,結果如下:表一
日期 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
天氣 | 晴 | 霾 | 霾 | 陰 | 霾 | 霾 | 陰 | 霾 | 霾 | 霾 | 陰 | 晴 | 霾 | 霾 | 霾 |
日期 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
天氣 | 霾 | 霾 | 霾 | 陰 | 晴 | 霾 | 霾 | 晴 | 霾 | 晴 | 霾 | 霾 | 霾 | 晴 | 霾 |
由于此種情況某市政府為減少霧霾于次年采取了全年限行的政策.
下表是一個調査機構對比以上兩年11月份(該年不限行![]() 天、次年限行
天、次年限行![]() 天共
天共![]() 天)的調查結果:
天)的調查結果:
表二
不限行 | 限行 | 總計 | |
沒有霧霾 |
| ||
有霧霾 |
| ||
總計 |
|
|
|
(1)請由表一數據求![]() ,并求在該年11月份任取一天,估計該市是晴天的概率;
,并求在該年11月份任取一天,估計該市是晴天的概率;
(2)請用統計學原理計算若沒有![]() 的把握認為霧霾與限行有關系,則限行時有多少天沒有霧霾?
的把握認為霧霾與限行有關系,則限行時有多少天沒有霧霾?
(由于不能使用計算器,所以表中數據使用時四舍五入取整數)
|
|
|
|
|
|
|
|
|
|
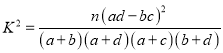
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=2cosxsin(x+ ![]() )﹣a,且x=﹣
)﹣a,且x=﹣ ![]() 是方程f(x)=0的一個解.
是方程f(x)=0的一個解.
(1)求實數a的值及函數f(x)的最小正周期;
(2)求函數f(x)的單調遞減區間;
(3)若關于x的方程f(x)=b在區間(0, ![]() )上恰有三個不相等的實數根x1 , x2 , x3 , 直接寫出實數b的取值范圍及x1+x2+x3的取值范圍(不需要給出解題過程)
)上恰有三個不相等的實數根x1 , x2 , x3 , 直接寫出實數b的取值范圍及x1+x2+x3的取值范圍(不需要給出解題過程)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=(log2x﹣2)(log4x﹣ ![]() )
)
(1)當x∈[2,4]時,求該函數的值域;
(2)若f(x)>mlog2x對于x∈[4,16]恒成立,求m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】袋子中有大小、質地相同的紅球、黑球各一個,現有放回地隨機摸取3次,每次摸取一個球,若摸出紅球,得10分,摸出黑球,得5分,則3次摸球所得總分至少是25分的概率是___.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知定義域為R的函數 ![]() 是奇函數.
是奇函數.
(1)求實數a,b的值;
(2)判斷f(x)在(﹣∞,+∞)上的單調性;
(3)若f(k3x)+f(3x﹣9x+2)>0對任意x≥1恒成立,求k的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com