
天水市第一次聯考后,某校對甲、乙兩個文科班的數學考試成績進行分析,
規定:大于或等于120分為優秀,120分以下為非優秀.統計成績后,
得到如下的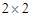 列聯表,且已知在甲、乙兩個文科班全部110人中隨機抽取1人為優秀的概率為
列聯表,且已知在甲、乙兩個文科班全部110人中隨機抽取1人為優秀的概率為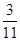 .
.
| | 優秀 | 非優秀 | 合計 |
| 甲班 | 10 | | |
| 乙班 | | 30 | |
| 合計 | | | 110 |
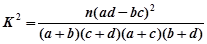 。
。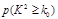 | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
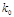 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
(1) 優秀 非優秀 合計 甲班 10 50 60 乙班 20 30 50 合計 30 80 110
(2)計算得到K2= ≈7.487<10.828.因此按99.9%的可靠性要求,不能認為“成績與班級有關系”
(3)抽到9號或10號的概率為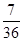 .
.
解析試題分析:
思路分析:此類問題(1)(2)直接套用公式,經過計算“卡方”,與數表對比,作出結論。(3)是典型的古典概型概率的計算問題,確定兩個“事件”數,確定其比值。
解:(1) 4分
(2)根據列聯表中的數據,得到K2= ≈7.487<10.828.因此按99.9%的 優秀 非優秀 合計 甲班 10 50 60 乙班 20 30 50 合計 30 80 110
可靠性要求,不能認為“成績與班級有關系” 8分
(3)設“抽到9或10號”為事件A,先后兩次拋擲一枚均勻的骰子,出現的點數為(x,y).所有的基本事件有:(1,1)、(1,2)、(1,3)、…、(6,6)共36個.事件A包含的基本事件有:(3,6)、(4,5)、(5,4)、(6,3)、(5,5)、(4,6)(6,4)共7個.所以P(A)= 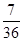 ,即抽到9號或10號的概率為
,即抽到9號或10號的概率為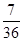 . 12分
. 12分
考點:“卡方檢驗”,古典概型概率的計算。
點評:中檔題,獨立性檢驗問題,主要是通過計算“卡方”,對比數表,得出結論。古典概型概率的計算中,常用“樹圖法”或“坐標法”確定事件數,以防重復或遺漏。


 長江作業本同步練習冊系列答案
長江作業本同步練習冊系列答案 小天才課時作業系列答案
小天才課時作業系列答案科目:高中數學 來源: 題型:解答題
在一次數學統考后,某班隨機抽取10名同學的成績進行樣本分析,獲得成績數據的莖葉圖如下.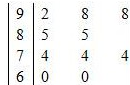
(Ⅰ)計算樣本的平均成績及方差;
(Ⅱ)現從80分以上的樣本中隨機抽出2名學生,求抽出的2名學生的成績分別在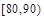 、
、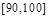 上的概率.
上的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某學生社團在對本校學生學習方法開展問卷調查的過程中發現,在回收上來的1000份有效問卷中,同學們背英語單詞的時間安排共有兩種:白天背和晚上睡前背。為了研究背單詞時間安排對記憶效果的影響,該社團以5%的比例對這1000名學生按時間安排類型進行分層抽樣,并完成一項實驗.實驗方法是,使兩組學生記憶40個無意義音節(如XIQ、GEH),均要求在剛能全部記清時就停止識記,并在8小時后進行記憶檢測。不同的是,甲組同學識記結束后一直不睡覺,8小時后測驗;乙組同學識記停止后立刻睡覺,8小時后叫醒測驗.
兩組同學識記停止8小時后的準確回憶(保持)情況如圖(區間含左端點而不含右端點).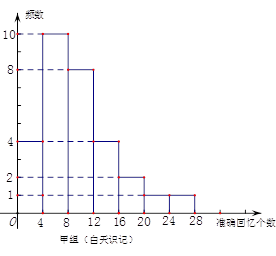
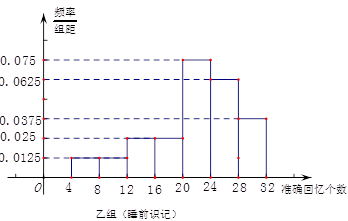
(1)估計這1000名被調查學生中停止后8小時40個音節的保持率不小于60%的人數;
(2)從乙組準確回憶單詞個數在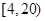 個范圍內的學生中隨機選2人,求能準確回憶
個范圍內的學生中隨機選2人,求能準確回憶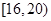 個單詞至少有一人的概率.
個單詞至少有一人的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
下表是某單位在2013年1—5月份用水量(單位:百噸)的一組數據:
月份 | 1 | 2 | 3 | 4 | 5 |
用水量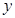 | 4 5 | 4 | 3 | 2 5 | 1 8 |
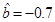 ,那么由該單位前4個月的數據中所得到的線性回歸方程預測5月份的用水量是否可靠?說明理由;
,那么由該單位前4個月的數據中所得到的線性回歸方程預測5月份的用水量是否可靠?說明理由;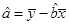 ,
,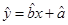
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
2012年第三季度,國家電網決定對城鎮居民民用電計費標準做出調整,并根據用電情況將居民分為三類: 第一類的用電區間在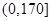 ,第二類在
,第二類在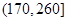 ,第三類在
,第三類在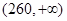 (單位:千瓦時). 某小區共有1000戶居民,現對他們的用電情況進行調查,得到頻率分布直方圖如圖所示.
(單位:千瓦時). 某小區共有1000戶居民,現對他們的用電情況進行調查,得到頻率分布直方圖如圖所示.
⑴ 求該小區居民用電量的中位數與平均數;
⑵ 本月份該小區沒有第三類的用電戶出現,為鼓勵居民節約用電,供電部門決定:對第一類每戶獎勵20元錢,第二類每戶獎勵5元錢,求每戶居民獲得獎勵的平均值;
⑶ 利用分層抽樣的方法從該小區內選出5戶居民代表,若從該5戶居民代表中任選兩戶居民,求這兩戶居民用電資費屬于不同類型的概率. 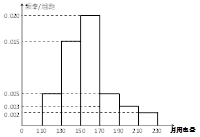
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
為了研究玉米品種對產量的影響,某農科院對一塊試驗田種植的一批玉米共10000 株的生長情況進行研究,現采用分層抽樣方法抽取50株作為樣本,統計結果如下:
| | 高莖 | 矮莖 | 合計 |
| 圓粒 | 11 | 19 | 30 |
| 皺粒 | 13 | 7 | 20 |
| 合計 | 24 | 26 | 50 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
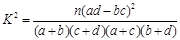 ,其中
,其中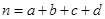 )
)查看答案和解析>>
科目:高中數學 來源: 題型:解答題
PM2. 5是指大氣中直徑小于或等于2.5微米的顆粒物,也稱為可入肺顆粒物。我國PM2.5標準采用世衛組織設定的最寬限值,即PM2.5日均值在35微克/立方米以下空氣質量為一級;在35微克/立方米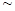 75微克/立方米之間空氣質量為二級;在75微克/立方米以上空氣質量為超標.
75微克/立方米之間空氣質量為二級;在75微克/立方米以上空氣質量為超標.
某試點城市環保局從該市市區2011年全年每天的PM2.5監測數據中隨機的抽取15天的數據作為樣本,監測值如莖葉圖所示(十位為莖,個位為葉)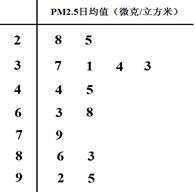
(1)從這15天的PM2.5日均監測數據中,隨機抽出三天,求恰有一天空氣質量達到一級的概率;
(2)從這15天的數據中任取三天數據,記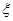 表示抽到PM2.5監測數據超標的天數,求
表示抽到PM2.5監測數據超標的天數,求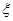 的分布列;
的分布列;
(3)以這15天的PM2.5日均值來估計一年的空氣質量情況,則一年(按360天計算)中平均有多少天的空氣質量達到一級或二級。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
從某學校的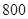 名男生中隨機抽取
名男生中隨機抽取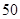 名測量身高,被測學生身高全部介于
名測量身高,被測學生身高全部介于 cm和
cm和 cm之間,將測量結果按如下方式分成八組:第一組[
cm之間,將測量結果按如下方式分成八組:第一組[ ,
, ),第二組[
),第二組[ ,
,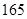 ),…,第八組[
),…,第八組[ ,
, ],右圖是按上述分組方法得到的頻率分布直方圖的一部分,已知第一組與第八組人數相同,第六組的人數為
],右圖是按上述分組方法得到的頻率分布直方圖的一部分,已知第一組與第八組人數相同,第六組的人數為 人.
人.
(Ⅰ)求第七組的頻率;
(Ⅱ)估計該校的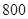 名男生的身高的中位數以及身高在
名男生的身高的中位數以及身高在 cm以上(含
cm以上(含 cm)的人數;
cm)的人數;
(Ⅲ)若從身高屬于第六組和第八組的所有男生中隨機抽取兩名男生,記他們的身高分別為 ,事件
,事件 {
{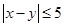 },事件
},事件 {
{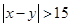 },求
},求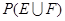 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
下表提供了某廠節能降耗技術改造后生產甲產品過程中記錄的產量x(t)與相應的生產能耗y(t標準煤)的幾組對照數據.
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
 ;
;查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com