欧美日韩激情,国产日韩欧美三级,日本久久二区

【題目】利用簡單隨機抽樣從某小區抽取100戶居民進行月用電量調查，發現其用電量都在50到350度之間，頻率分布直方圖如圖所示．在這些用戶中，用電量落在區間[150，250]內的戶數為（）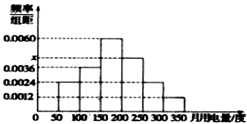

A.46
B.48
C.50
D.52

【答案】D
【解析】解：這些用戶中，用電量落在區間[150，250]內的頻率為1﹣（0.0024+0.0036+0.0024+0.0012）×50=0.52
∴用電量落在區間[150，250]內的戶數為
100×0.52=52．
故選：D．
【考點精析】關于本題考查的頻率分布直方圖，需要了解頻率分布表和頻率分布直方圖，是對相同數據的兩種不同表達方式.用緊湊的表格改變數據的排列方式和構成形式，可展示數據的分布情況.通過作圖既可以從數據中提取信息，又可以利用圖形傳遞信息才能得出正確答案．

練習冊系列答案

金考卷初中畢業學業考試說明檢測卷系列答案

數學中考模擬試題系列答案

金考卷著名重點中學領航中考沖刺試卷系列答案

湖南中考必備系列答案

年級	高中課程	年級	初中課程
高一	高一免費課程推薦！	初一	初一免費課程推薦！
高二	高二免費課程推薦！	初二	初二免費課程推薦！
高三	高三免費課程推薦！	初三	初三免費課程推薦！
更多初中、高中輔導課程推薦,點擊進入>>

相關習題

科目：高中數學 來源： 題型：

【題目】已知兩點A（﹣2，0），B（0，2），點C是圓x2+y2﹣2x=0上的任意一點，則△ABC的面積最小值是．

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】已知曲線C的極坐標方程是ρ＝2,以極點為原點,極軸為x軸的正半軸建立平面直角坐標系,直線l的參數方程為(t為參數).

(1)寫出直線l的普通方程與曲線C的直角坐標方程;

(2)設曲線C經過伸縮變換得到曲線,設M(x,y)為上任意一點,求的最小值,并求相應的點M的坐標.

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】已知函數.

（1）討論函數的單調性；

（2）當時，若函數的導函數的圖象與軸交于，兩點，其橫坐標分別為，，線段的中點的橫坐標為，且，恰為函數的零點，求證： .

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】已知集合A={x|1≤x≤5}，B={x|log2x＞1}
（1）分別求A∩B，（RB）∪A；
（2）已知集合C={x|2a﹣1≤x≤a+1}，若CA，求實數a的取值范圍．

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】已知函數f（x）=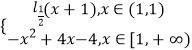
（1）在給定直角坐標系內直接畫出f（x）的草圖（不用列表描點），并由圖象寫出函數 f（x）的單調減區間；

（2）當m為何值時f（x）+m=0有三個不同的零點．

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】銷售甲、乙兩種商品所得利潤分別是y1 ， y2萬元，它們與投入資金x萬元的關系分別為y1=m +a，y2=bx，（其中m，a，b都為常數），函數y1 ， y2對應的曲線C1 ， C2如圖所示．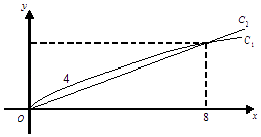

（1）求函數y1與y2的解析式；
（2）若該商場一共投資10萬元經銷甲、乙兩種商品，求該商場所獲利潤的最大值．