
【題目】最近幾年汽車金融公司發展迅猛,主要受益于監管層面對消費進人門檻的降低,互聯網信貸消費的推廣普及,以及汽車銷售市場規模的擴張.如圖是2013﹣2017年汽車金融行業資產規模統計圖(單位:億元).
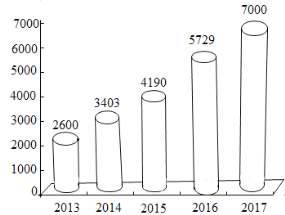
(1)以年份值2013,2014,…為橫坐標,汽車金融行業資產規模(單位:億元)為縱坐標,求y關于x的線性回歸方程;
(2)利用(1)中的回歸方程,預計2018年汽車金融行業資產規模(精確到億元).
附:回歸直線的斜率和截距的最小二乘估計公式分別為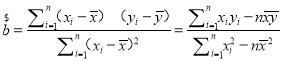 ,
,![]() (其中
(其中![]() ,
,![]() 為樣本平均值).
為樣本平均值).
參考數據:![]() 4.620×107,2015
4.620×107,2015![]() 4.619×107.
4.619×107.
科目:高中數學 來源: 題型:
【題目】已知函數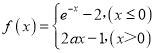 (a是常數且a>0).對于下列命題:
(a是常數且a>0).對于下列命題:
①函數f(x)的最小值是-1;
②函數f(x)在R上是單調函數;
③若f(x)>0在![]() 上恒成立,則a的取值范圍是a>1;
上恒成立,則a的取值范圍是a>1;
④對任意的x1<0,x2<0且x1≠x2,恒有
![]() .
.
其中正確命題的序號是____________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)是定義在(-∞,0)∪(0,+∞)上的偶函數,當x>0時,f(x)=lnx-ax,若函數在定義域上有且僅有4個零點,則實數a的取值范圍是( )
A.(e,+∞)B.(0,![]() )
)
C.(1,![]() )D.(-∞,
)D.(-∞,![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設![]() 分別是橢圓
分別是橢圓![]() 的左、右焦點,已知橢圓的長軸為
的左、右焦點,已知橢圓的長軸為![]() 是橢圓
是橢圓![]() 上一動點,
上一動點,![]() 的最大值為
的最大值為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)過點![]() 的直線
的直線![]() 交橢圓
交橢圓![]() 于
于![]() 兩點,
兩點,![]() 為橢圓
為橢圓![]() 上一點,
上一點,![]() 為坐標原點,且滿足
為坐標原點,且滿足![]() ,其中
,其中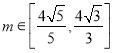 ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在南北方向有一條公路,一半徑為100![]() 的圓形廣場(圓心為
的圓形廣場(圓心為![]() )與此公路所在直線
)與此公路所在直線![]() 相切于點
相切于點![]() ,點
,點![]() 為北半圓弧(弧
為北半圓弧(弧![]() )上的一點,過點
)上的一點,過點![]() 作直線
作直線![]() 的垂線,垂足為
的垂線,垂足為![]() ,計劃在
,計劃在![]() 內(圖中陰影部分)進行綠化,設
內(圖中陰影部分)進行綠化,設![]() 的面積為
的面積為![]() (單位:
(單位:![]() ),
),
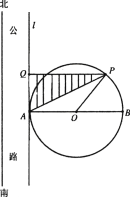
(1)設![]() ,將
,將![]() 表示為
表示為![]() 的函數;
的函數;
(2)確定點![]() 的位置,使綠化面積最大,并求出最大面積.
的位置,使綠化面積最大,并求出最大面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數![]() ,其中
,其中![]() 是自然對數的底數.
是自然對數的底數.
(1)若![]() ,
,![]() ,證明
,證明![]() ;
;
(2)是否存在實數![]() ,使得函數
,使得函數![]() 在區間
在區間![]() 上有兩個零點?若存在,求出
上有兩個零點?若存在,求出![]() 的取值范圍:若不存在,請說明理由.
的取值范圍:若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】天干地支紀年法,源于中國,中國自古便有十天干與十二地支.十天干:甲、乙、丙、丁、戊、己、庚、辛、壬、癸.十二地支:子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥.天干地支紀年法是按順序以一個天干和一個地支相配,排列起來,天干在前,地支在后,天干由“甲”起,地支由“子”起,比如第一年為“甲子”,第二年為“乙丑”,第三年為“丙寅”,…,以此類推,排列到“癸酉”后,天干回到“甲”重新開始,即“甲戌”,“乙亥”,之后地支回到“子”重新開始,即“丙子”,…,以此類推,已知2016年為丙申年,那么到改革開放100年時,即2078年為________年
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 是梯形,
是梯形,![]() ,
,![]() ,
,![]() 是正三角形,
是正三角形,![]() 為
為![]() 的中點,平面
的中點,平面![]() 平面
平面![]() .
.
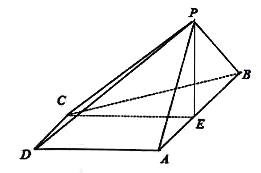
(1)求證:![]() 平面
平面![]() ;
;
(2)在棱![]() 上是否存在點
上是否存在點![]() ,使得二面角
,使得二面角![]() 的余弦值為
的余弦值為![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com