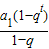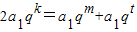設等比數列{an}的前n項的和為Sn,公比為q(q≠1).
(1)若S4,S12,S8成等差數列,求證:a10,a18,a14成等差數列;
(2)若Sm,Sk,St(m,k,t為互不相等的正整數)成等差數列,試問數列{an}中是否存在不同的三項成等差數列?若存在,寫出兩組這三項;若不存在,請說明理由;
(3)若q為大于1的正整數.試問{an}中是否存在一項ak,使得ak恰好可以表示為該數列中連續兩項的和?請說明理由.
【答案】
分析:(1)根據S
4,S
12,S
8成等差數列,q≠1,可得S
12=S
4+S
8,化簡可得2q
8=1+q
4,進而可以證明a
10,a
18,a
14成等差數列;
(2)根據S
m,S
k,S
t(m,k,t為互不相等的正整數)成等差數列,可得2S
k=S
m+S
t,化簡可得
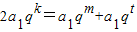
,從而可得a
m+1,a
k+1,a
t+1成等差數列,即可得出結論;
(3)假設存在一項a
k,使得a
k恰好可以表示為該數列中連續兩項的和,設a
k=a
n+a
n+1,可得k>n,q
k-n=1+q
,從而可得結論.
解答:解:(1)若S
4,S
12,S
8成等差數列,q≠1,則S
12=S
4+S
8,
∴
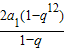
=
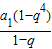
+
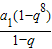
∴2q
8=1+q
4∴a
10+a
14=
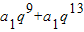
=
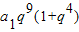
=
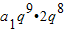
=2a
18,
∴a
10,a
18,a
14成等差數列;
(2)若S
m,S
k,S
t(m,k,t為互不相等的正整數)成等差數列,則2S
k=S
m+S
t,
∴
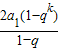
=
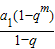
+
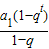
∴2q
k=q
m+q
t∴
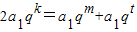
∴a
m+1,a
k+1,a
t+1成等差數列,
∴a
m+2,a
k+2,a
t+2成等差數列;
(3)假設存在一項a
k,使得a
k恰好可以表示為該數列中連續兩項的和,設a
k=a
n+a
n+1,
則

∵a
1≠0,q>1
∴q
k-1=q
n-1+q
n∴q
k=q
n+q
n+1∵q
n+1>1
∴q
k>q
n∴k>n,q
k-n=1+q
當q為偶數時,q
k-n為偶數,而1+q為奇數,假設不成立;
當q為奇數時,q
k-n為奇數,而1+q為偶數,假設也不成立,
綜上,{a
n}中不存在a
k,使得a
k恰好可以表示為該數列中連續兩項的和.
點評:本題考查等差數列與等比數列的綜合,考查等差數列的證明,考查學生分析解決問題的能力,屬于中檔題.

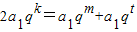 ,從而可得am+1,ak+1,at+1成等差數列,即可得出結論;
,從而可得am+1,ak+1,at+1成等差數列,即可得出結論;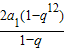 =
=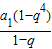 +
+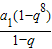
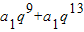 =
=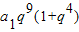 =
=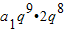 =2a18,
=2a18,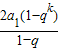 =
=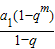 +
+