Question

拋物線y²=8x上的點P到兩直線l₁：x=-2，l₂：12x-5y+15=0的距離之和的最小值為

3

．

Answer 1

分析：由拋物線方程求出其焦點坐標和準線方程，把拋物線y²=8x上的點P到兩直線l₁：x=-2，l₂：12x-5y+15=0的距離之和的最小值轉化為焦點到l₂：12x-5y+15=0的距離，由點到直線的距離公式求解．

解答：解：如圖，

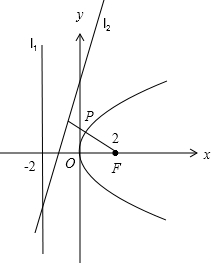
由拋物線y²=8x，得其焦點F（2，0），準線方程為x=-2．
∴l₁：x=-2為拋物線的準線，
P到兩直線l₁：x=-2，l₂：12x-5y+15=0的距離之和即為P到F和l₂：12x-5y+15=0的距離之和．
最小值為F到l₂：12x-5y+15=0的距離，等于

|12×2-5×0+15|

122+(-5)2

=

39

13

=3．
故答案為3．

點評：本題考查了直線與圓錐曲線的關系，考查了數形結合的解題思想方法和數學轉化思想方法，是中檔題．